Two-way ANOVA는 논문 연구주제부터 실무에서까지 굉장히 많이 쓰이는 통계 분석 방법이다. 이원배치분산분석의 개념을 아주 쉽게 설명하는 것부터 시작하여 Stats모델을 통한 코드 및 결과해석 실습까지 해보고자 한다.
목차
1. 이원배치분산분석의 분석 과정 안내
2. 이원분산분석(Two-way ANOVA)의 통계적 개념, 사전 조건, 그리고 가설
3. 기초 데이터셋 설명 및 전처리 안내 - 쉽게 따라하기
4. 상호작용(Interaction Effect)를 통한 결과 해석
이원배치분산분석의 분석 과정 안내

- 이원배치분산 분석, 왜 그리고 언제 써야 쓰는 모델인가
이원배치분산 분석은 독립변수(범주형 척도)가 2개이고 종속변수(연속형 척도)가 하나일 때 독립변수 간에 나타나는 상호작용을 검증해보기 위해서 사용되는 모델이다. 단순히 Group이 많다고 쓰는 것이 아니라, 단일 그룹에서는 효과가 없다가 두 그룹 이상이 서로 영향을 받을 때 나타나는 고유의 효과를 보기위해서 쓰는 것이다.
예를 들어, 유치원 A와 유치원 B가 있고(독립변수1은 유치원), 영양사1과 영양사2가 (독립변수2는 영양사) 있다고 해보자. 이때 부모님의 관심은 아이들 키(종속변수는 아이들의 키)가 관심이 있을 것이다. 만약 어떤 유치원을 다니든, 어느 영양사의 급식을 먹든 아이들의 키가 비슷하게 큰다면 별로 관심이 없을 것이다.
그러나 만약 유치원A에 다니면서 영양사2의 급식을 먹은 아이들이 또래 애들보다 키가 월등히 크다면, 부모들의 엄청난 관심을 갖게 될 것이다. 도대체 유치원A만 다녀서도 안 되고 영양사2의 급식을 먹어서도 안 되고, 오직 둘 간의 조합이 있을 때만 월등히 키가 더 크게 되는 것인가? 이러한 질문들에 대한 해답을 내려줄 수 있는 것이 Two-way ANOVA의 핵심이다.
이원분산분석(Two-way ANOVA)의 통계적 개념, 사전 조건, 그리고 가설
(1) Two-way ANOVA의 통계적 개념
| 변인 요소 | 자유도 | Sum of Square | Mean Square | F-Ratio |
| 독립변수1(A) | k-1 | SSA | MSA | MSA / MSE |
| 독립변수2(B) | l-1 | SSB | MSB | MSB / MSE |
| 상호작용 (변수1 X 변수2) |
(k-1)*(l-1) | SS AB | MSAB | MSAB / MSE |
| 오차(Error) | kl(m-1) | SSE | MSE | - |
| 총합 | klm-1 | SST | - | - |
| 최종 수식: Y = u + A + B + A*B + Error SST = SSa + SSb + SS_ab + SSe |
||||
ANOVA 모델에서 가장 핵심적인 사항은 F-Ratio임에는 변함이 없다. 아주 쉽게 말해서 F-Ratio란 그룹 간 변동성 (Between Variance)가 그룹 내 변동성(Within Variance)보다 커야 한다는 의미이다. 이원배치분산분석에서는 Within Variance를 따질 때 자연오차로 발생한 MSE값을 기준으로 F-Ratio를 산출하고, 그 최소한 비율이 1은 넘어야지 의미있는 것으로 간주한다.
그 중에서도 가장 핵심적인 것은 바로 상호작용에 해당하는 MSAB / MSE 값이 1이 넘고, 유의한지를 봐야하는 것이다. 왜냐하면 위에서 말했듯이 우리는 변수끼리 어떤 영향을 주는지 보는 것이 모델 사용 이유이기 때문이다. 따라서 이 관점에서 결과 해석에도 한 번 반영해보겠다.
(2) Two-way ANOVA의 사전 조건
- ANOVA의 사전조건 총 정리
- 독립변수는 범주형 척도를 가져야 한다.
- 종속변수는 연속형 척도를 가져야 한다.
- 모든 집단은 등분산성을 보여야 한다.
- Python 환경에서는 from scipy import stats 중에서 bartlett Test를 통해 검증할 수 있다.
- Bartlett Test에서 산정하는 가정을 볼 때는 조심해서 봐야한다.
H0: 변수 간 분산에 유의미한 차이가 없을 것이다.
H1: 변수 간 분산에 유의미한 차이가 있을 것이다.
쉽게 말해서 등분산성 검정에서는 H0을 채택하고, H1을 기각하는 결론을 얻어야 이상적이다.
- 각 변수의 분포는 정규성을 보여야 한다.
- 정규성 검정은 Shaprio Test를 통해서 할 수 있다.
- 정규성 검정을 통과하지 못 하더라도, 왜도의 절대값이 2를 넘지 않으면 Test 진행하는 경우도 많다.
(3) Two-way ANOVA의 귀무가설과 대립가설
가설에 대해서 다소 헷갈려하는 사람들이 있기에 여기에서 아주 쉽게 정리해보고자 한다. 헷갈리는 것 중 하나는 연구자가 세우는 "연구 가설"과 ANOVA에서 가정하는 "모델 가설"이 같다고 생각하는 것이다. 이거는 아주 단순하게 풀어볼 수 있다. 결론부터 얘기하면 먼저 연구 가설을 세운 후 모델을 돌려봤을 때, 내 연구에서 주장하는 가설대로 모델의 결과가 나오는지 확인해 봐야 한다.
- 연구 가설의 예시
- 변수1과 변수2는 상호 작용 효과를 보일 것이다.
- ANOVA 모델의 가설 정리
- 귀무가설: 모든 집단 간 평균에는 유의미한 차이가 없을 것이다.
- 대립가설: 적어도 하나는 유의미한 차이가 있을 것이다.
- 결과 해석 가이드
- 모델 결과가 유의했을 때, 모든 집단 간 평균이 같지 않다는 사실만 확인한 것이지, 어디서 어떻게 더 높고 낮은지는 알 수가 없는 상태이다.
- 따라서 연구가설까지 Fact Check를 하려면 반드시 Post-Hoc(사후 검정)까지 진행해야 결과를 제대로 해석할 수 있는 것이다.
기초 데이터셋 설명 및 전처리 안내
(1) 이원배치 분산분석 예시 데이터 간단 소개
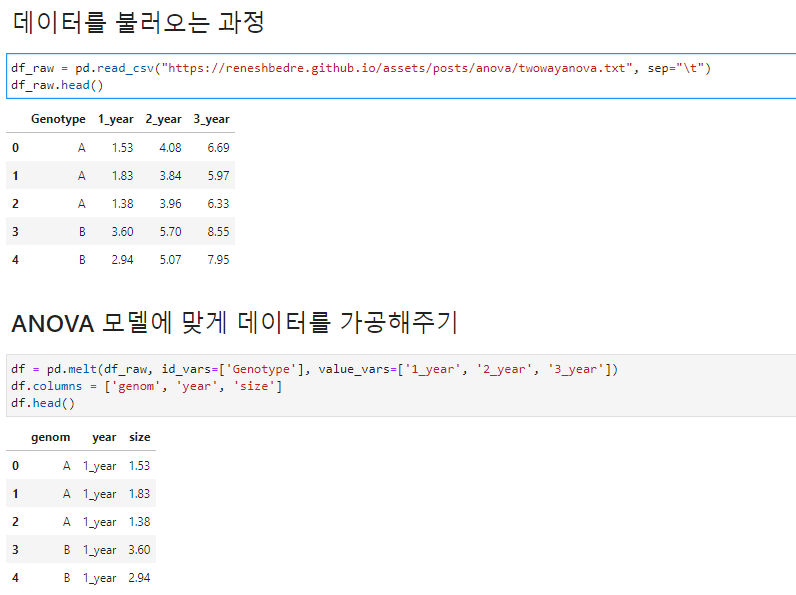
이번에 사용할 데이터는 곤충의 유전자 유형과 성장시기에 따른 크기 차이를 보는 것이다. 독립변수1은 곤충의 유전자 유형이고, 독립변수 2는 성장시기가 되고, 마지막으로 독립변수는 곤충의 크기가 된다. 원본 데이터를 받을 수 있는 주소는 여기에 남겨둘테니 편하게 복사 붙여 넣기해서 쓰도록 하자.
참고로 ANOVA에서는 데이터셋을 받아올 때 두 번째 Cell처럼 데이터 형태를 변환해주어야 한다. 여기서 활용한 데이터 전처리 방법은 pandas.melt를 활용해주었다. 아주 간단하게 설명하면 피벗 테이블로 만드는 과정을 반대로 하는 메소드라고 생각하면 편하다. 하지만 여기서는 이 메소드에 대해서 자세하게 다루지는 않도록 하겠다.
(2) 예시 데이터 설정할 수 있는 가설 및 결과 해석 가이드
- 연구 가설: 유전자 유형과 성장시기에는 특별한 상호작용이 발생할 것이다.
- 이원분산 분석 모델의 가설
- H0: 모든 집단 간 곤충 크기에는 유의미한 차이가 없을 것이다.
- H1 적어도 한 개의 집단에서는 유의미한 차이가 발생할 것이다.
- 이원분산분석 사후 검정 가설
- 특별히 더 연구에 맞는 유전자 및 성장시기에서만 관측할 수 있는 효과가 있을 것이다 .
- 따라서 누가 더 높고 낮은지 세부적인 분석을 실시하도록 한다.
이원분산분석(Two-way ANOVA) 을 위한 Python 코드
(1) Python으로 실시하는 이원분산분석
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
import statsmodels.api as sm
from statsmodels.formula.api import ols
## Two-way ANOVA에 맞는 수식을 설정하는 코드
two_way_anova = ols('size ~ C(genom) + C(year) + C(genom):C(year)'
, data = df).fit()
## 결과 해석을 저장하는 코드
result = sm.stats.anova_lm(two_way_anova)
## 결과 요약
print(result)
df sum_sq mean_sq F PR(>F)
C(genom) 5.0 58.551733 11.710347 32.748581 1.931655e-12
C(year) 2.0 278.925633 139.462817 390.014868 4.006243e-25
C(genom):C(year) 10.0 17.122967 1.712297 4.788525 2.230094e-04
Residual 36.0 12.873000 0.357583 NaN NaN
|
cs |
- Python 코드해설
- 첫 번째는 모델에서 사용할 수식과 데이터를 입력하고, 학습을 진행하는 것이 목적이다.
- 두 번째는 모델에서 뱉은 결과를 저장하여, 한 번에 해석할 수 있는 형태로 데이터를 반환하는 것이다.
(2) Tukey's HSD를 통한 사후 분석 실시
- Step1. Two-way ANOVA에서 정의하는 상호작용 효과(Interaction Effect)
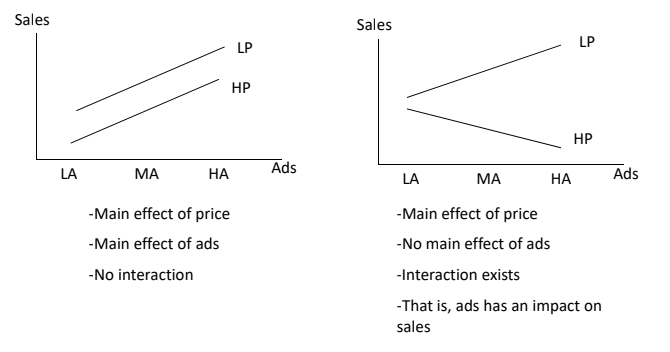
이원분산분석에서 정의하는 상호작용 효과는 단일변수에서는 나타나지 않지만, 두 변수 간의 조합이 만들어내는 결과를 의미한다. 왼쪽 사진에서 보면 광고와 가격 모두 판매에 영향을 주지만, 변수 간 조합에서 특이점을 보이지 않기에 평행이동하는 패턴을 보여준다. 반면에 오른쪽 그래프에서는 광고 단일 변수로는 효과가 없지만, 가격이라는 변수가 들어오면 특이한 패턴을 만들어내는 것을 볼 수 있다.
- Step2. Two-way ANOVA에서 정의하는 상호작용 효과(Interaction Effect)
|
1
2
3
4
5
6
7
8
9
10
11
|
from statsmodels.graphics.factorplots import interaction_plot
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (12, 9)
fig = interaction_plot(x=df['genom']
, trace = df['year']
, response=df['size'],
)
plt.title("Checking Interaction size", fontsize = 25, pad = 10)
plt.grid(alpha = 0.4);
|
cs |

유전자 A와 B를 보면 유전자 유형과 성장시기 모두 Main Effect는 있지만, 상호작용은 볼 수 없다. 반면에 유전자 D와 E 간에는 성장시기에 따른 뚜렷한 상호 작용 효과를 볼 수 있다. 따라서 사후검정에서도 이 영역에 Focus를 두고 상호 작용 테스트를 진행힌다. 이번 실험에서는 유전자 D와 E 중 성장시기 3_year에서 나타나는 상호작용 효과가 유의한지 보는 것에 초점을 맞출 것이다.
참고로 존재하는 21개의 데이터 포인트에서 사후검정을 진행하면 총 21C2 = 210개의 조합을 확인해야 한다. 이것은 매우 비효율적이니 원하는 영역에 집중하여 데이터를 검증하는 것을 권장한다.
- Step3. Tukey HSD 사후 분석을 통한 상호작용 효과(Interaction Effect) 검증
- 코드해설
- part1은 모든 상호작용을 확인하기 위해서 변수 간 조합에서 나타날 수 있는 모든 집단을 정의하였다.
- part2에서는 원하는 영역을 선택하기 위해서 pandas의 query문을 활용하였다. Query문의 자세한 사항은 이 포스팅을 참고하길 바란다.
- 마지막에는 사후 검정 결과를 확인한 결과 우리가 원하는 유전자 D와 E 사이에서는 유의한 검증 결과를 얻을 수 있었다.
- 코드해설
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
## part1 상호 작용을 확인하기 위해서 모든 집단을 정의하는 코드
df['group_combination'] = df.genom + '-' + df.year
## part2 Tukey 사후 검정을 하기 위한 모델 선언
hsd = pairwise_tukeyhsd( df.query('genom == ["D", "E"]')['size']
, df.query('genom == ["D", "E"]')['group_combination'])
## 사후 검정 결과 확인
hsd_summary = hsd.summary()
hsd_summary
Multiple Comparison of Means - Tukey HSD, FWER=0.05
group1 group2 meandiff p-adj lower upper reject
D-3_year E-1_year -8.61 0.001 -10.7695 -6.4505 True
D-3_year E-2_year -5.3 0.001 -7.4595 -3.1405 True
D-3_year E-3_year -3.65 0.0011 -5.8095 -1.4905 True
|
cs |
이제 남은 것은 ANOVA 결과를 우리 가설에 맞게 해석하는 것만 남았다. 우리의 연구가설은 "특별한 상호작용이 나타나는 영역을 발견"하는 것이었다. 확인한 결과는 모든 성장시기에서 유전자 D & E 간에는 특별한 Interaction Effect가 있음을 발견했다. 이에 대한 첫 번째 근거는 ANOVA 모델에서 H0를 기각하여, 집단 간 평균에는 차이가 있음을 발견한 것이다. 두 번째 근거는 Tukey HSD 사후 분석 결과 모든 Data 집단에서 Mean Difference가 유의한 것을 발견했다. 따라서 우리의 연구가설은 Fact라고 결론 지을 수 있는 것이다.
그대들의 논문과 과제에 도움이 되었길 바란다.
'통계학 기초' 카테고리의 다른 글
| 회귀모델 평가를 위한 통계 오차 지표 모음(MSE, MAE, RMSE 등 5개 지표) (1) | 2024.02.06 |
|---|---|
| [Python]독립표본(Independent Samples) T-Test를 활용한 A/B Test 검증(코드부터 결과 해석까지 한 번에) (1) | 2023.10.04 |
| [Python] 카이제곱 독립성 검정을 활용한 데이터 분석(feat. A/B Test까지) (0) | 2022.08.30 |
| [Python] COHORT 분석 개념부터 실전 코드까지 (feat. 분석 예제 포함) (0) | 2022.08.18 |
| [Python]베이지안 A/B Test로 기대수익과 기대손실 계산하는 방법 (0) | 2022.08.11 |



