이번 포스팅에서는 베이지안 A/B Test를 수행한 이후 기대 수익을 계산하는 방법에 대해서 얘기해보고자 한다. 기존에는 결과 값이 0과 1로 boolean 값이기 때문에 Beta 분포를 사전분포로 활용했었다. 그러나 기대수익은 단위당 수익을 나타내는 양의 실수이기 때문에 동일한 분포를 적용할 수 없는 문제가 생긴다. 이러한 문제를 Gamma 분포와 베이지안 추론을 통해서 해결하는 방법을 Python기반으로 소개해보고자 한다.
1. 이론적 방법 소개 - 감마분포를 통한 기대수익 산출 방법
(1) 베이지안 추론 - Prior 변수 설명
우리는 이번 목적이 기대수익을 창출하는 것이다. 아주 간단한 아이디어부터 시작을 해보자. 1,000명의 사람이 들어왔을 때 만약 100명이 구매를 했고, 1명당 평균 수익이 2만원이라고 해보자. 이러한 실험에서 기대할 수 있는 수익은 100명 * 2만원 = 2,000,000원이 될 것이다. 이 예시에서 알 수 있듯이, 기대되는 수익률에서 중요한 것은 바로 전환율과 단위당 평균 수익인 것이다. 이 개념을 보다 통계적 수식으로 표현해보고자 한다.
- 기대 수익(Expected Revenue) 계산 방법 및 변수 정리
- 아이디어: 기대수익 = 기대되는 전환율 * 기대되는 단위당 수익
- 통계 수식: E(R) = E(X) (전환율) * E(Y) ( 단위 당 수익) = 𝜆𝑖 * 1/𝜃𝑖
- 전환율(conversion Rate) 𝜆𝑖: X ~ Beta( α, β )
- 개념: 베이지안 추론에서 가장 대표적으로 사용되는 Beta분포이다. 베타 분포를 사용하는 이유는 0과 1로 표현되는 종속변수에서 우리가 모수라고 생각하는 Posterior를 계산하는데 가장 적합한 확률분포이기 때문이다.
- α(알파): 흔히 실험에서 성공한 횟수를 의미한다. 이번 예시에서는 구매를 한 100명 고객 수에 해당한다.
- β(베타): 알파와는 반대로 실험에서 실패한 횟수를 의미한다. 예시에서 구매를 하지 않은 900명의 고객이다.
- λ(람다): 베타 분포에서 예측되는 기대 전환 확률을 의미하고, 사후 확률 분포 계산할 때 아주 중요하게 사용될 파라미터이니 잘 기억해야 한다.
- i번째 항목의 기대 전환율: 𝐸(𝑋𝑖)=𝜆𝑖
- 단위 당 수익(Revenue per Unit) 𝜃𝑖: Y ~ Gamma( α, Θ )
- 개념: 감마분포는 변수가 양의 실수일 때, 지수 분포의 형태로 데이터를 설명하는 확률분포 모형이다. 단위 당 수익을 계산할 때 베이지안 추론에서 가장 대표적으로 사용하는 Probability Density Function이다.
- α(알파): 감마분포의 형상모수로 전체적인 확률분포의 모양을 결정하는 파라미터이다. 베이지안 추론 환경에서는 베타와 마찬가지로 실험에 성공한 횟수를 의미한다.
- Θ(세타): 가마분포의 척도모수로 분포의 분산, 즉 얼마나 분포가 퍼져있는지 결정하는 파라미터이다. 베이지안 추론 환경에서는 단위 당 수익(Revenue per Unit)이 여기에 들어가게 된다.
- i번째 항목의 기대 단위당 수익: 𝐸(𝑋𝑖) = 1/𝜃𝑖
- 감마분포는 지수함수의 형태를 하고 있기 때문에 기대 세타값이 위와 같이 계산되어야 한다.
- 이에 대해서 보다 궁금한 사람이 있다면, VWO에서 배포한 논문 중 B 부분을 참고하면 더욱 도움이 될 것이다.
2. Python 코드를 통한 베이지안 기대이익 계산
(1) 사전 데이터 준비
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
## Data Columns
col = ['sample_size', 'converted', 'revenue', 'cvr', 'aov']
idx = ['variant_a', 'variant_b']
a_result_dict = {
'sample_size': 2743
, 'converted': 895
, 'revenue': 44702
, 'cvr': 895/2743
, 'aov': 44702 / 895
}
b_result_dict = {
'sample_size': 2358
, 'converted':772
, 'revenue': 45123
, 'cvr': 772/2358
, 'aov': 45123 / 772
}
a_results = pd.DataFrame([a_result_dict])
b_results = pd.DataFrame([b_result_dict])
results = pd.concat([a_results, b_results], axis = 0)
results.index = idx
|
cs |
| Group | Sample Size | Converted | Revenue | CVR | Revenue per Order (AOV) |
| Variant A | 2,743 | 895 | $ 44,702 | 0.326285 | $ 49.946 |
| Variant B | 2,358 | 772 | $ 45,123 | 0.327396 | $ 58.449 |
이번 A/B Test에서 Group A와 Group B를 각 샘플 사이즈는 2,743명과 2,358명이라고 가정해보자. 이때 각각 895명과 772명이 실제로 구매 전환까지 이루어졌다고 가정했을 때 총 수익률, 전환율, 그리고 구매당 단가를 계산했을 때 위와 같은 데이터를 볼 수 있다.
( ※ AOV의 정의: Average Order Value로 다른 말로 Revenue per Order 등으로 표현한다. 한국어로 번역하면 구매 당 단가로 편하게 이해할 수 있다.)
(2) 전환율 계산 코드 및 기초 시각화
- 학습 결과로 Conversion Prior Distribution 업데이트
- Control Group ~ Beta( α + 전환된 수 , β + 전환하지 못 한 수 )
- Treatment Group ~ Beta( α +전환된 수 , β + 전환하지 못 한 수 )
- 사전 전환율은 모르고 있기 때문에 α,β 파라미터 값은 모두 1로 지정하여 uniform distribution을 가정한다.
- Control Group ~ Beta( α + 전환된 수 , β + 전환하지 못 한 수 )
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
## Generating Beta Distribution with Prior Data
control_cr = beta(1 + results.loc['variant_a', 'converted'], 1 + results.loc['variant_a', 'sample_size'] - results.loc['variant_a', 'converted'])
treatment_cr = beta(1 + results.loc['variant_b', 'converted'], 1 + results.loc['variant_b', 'sample_size'] - results.loc['variant_b', 'converted'])
plt.rcParams['figure.figsize'] = (12, 8)
x = np.linspace(0,1,1000)
plt.plot(x, control_cr.pdf(x), label='control')
plt.plot(x, treatment_cr.pdf(x), label='treatment')
plt.xlim(0.25, 0.40)
plt.xlabel('Conversion Probability')
plt.ylabel('Density')
plt.title('Experiment Posteriors')
plt.legend()
plt.grid(alpha = 0.4, linestyle = '--')
## Conversion Distribution based on Beta control_conversion_simulation = np.random.beta(1 + results.loc['variant_a', 'converted'] , 1 + results.loc['variant_a', 'sample_size'] - results.loc['variant_a', 'converted'] , size=100000) treatment_conversion_simulation = np.random.beta(1 + results.loc['variant_b', 'converted'] , 1 + results.loc['variant_b', 'sample_size'] - results.loc['variant_b', 'converted'] , size=100000) (control_conversion_simulation > treatment_conversion_simulation).mean() |
cs |

전환율의 결과로만 봤을 때는 Group A와 Group B 차이가 없는 것으로 보여진다. 실제 P(Control > Treatment) 확률은 약 46%로 계산이 된다. 이 수치를 해석할 때는 A와 B 확실한 우승자가 없다고 해석해야 할 것이다. 하지만 기대수익을 계산하는 순간 실험 결과 해석은 완전히 뒤바뀌게 될 수도 있다.
(3) 기대이익 Simulation Analysis
3-1) 기대수익 계산을 위한 코드 해설
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
## Part1. Conversion Distribution based on Beta
control_conversion_simulation = np.random.beta(1 + results.loc['variant_a', 'converted']
, 1 + results.loc['variant_a', 'sample_size'] - results.loc['variant_a', 'converted']
, size=100000)
treatment_conversion_simulation = np.random.beta(1 + results.loc['variant_b', 'converted']
, 1 + results.loc['variant_b', 'sample_size'] - results.loc['variant_b', 'converted']
, size=100000)
## Part2. Revenue Distribution based on Gamma
control_revenue_simulation = np.random.gamma(shape = (0.1 + results.loc['variant_a', 'converted'])
, scale = (0.1 / (1 + (0.1)*results.loc['variant_a', 'converted']*results.loc['variant_a', 'aov']))
, size=100000)
treatment_revenue_simulation = np.random.gamma(shape=(0.1 + results.loc['variant_b', 'converted'])
, scale=(0.1/(1 + (0.1)*results.loc['variant_b', 'converted']*results.loc['variant_b', 'aov']))
, size=100000)
## Part3. Generating revenue per session
control_avg_purchase = [i/j for i,j in zip(control_conversion_simulation, control_revenue_simulation) ]
treatment_avg_purchase = [i/j for i,j in zip(treatment_conversion_simulation, treatment_revenue_simulation)]
|
cs |
위에서 언급했듯이, 기대수익을 계산하는 방법은 아래의 수식을 따라야 한다.
- 통계 수식: E(R) = E(X) (전환율) * E(Y) ( 단위 당 수익) = 𝜆𝑖 * 1/𝜃𝑖
- Part1. 전환율 Simulation 계산 방법
- 전환율은 사전 파라미터 ( α = 1, β = 1)를 가정하고 Posterior 정보를 학습한 베타분포를 따르기 때문에 Part1의 코드가 구성 되었다. 아직 이 말이 어렵게 다가온다면 이전 포스팅을 참고하면 정확하게 이해가 될 것이다.
- Part2. 단위 당 수익을 계산하기 위한 감마 분포 계산 방법
- 감마 분포는 사전 파라미터터는 각각 0.1, 0.1로 할당하게 된다.
- 이후 학습된 데이터를 계산할 때는 지수함수 이기에 아래의 수식과 같이 계산을 해주어야 한다.
- θ | c,s ~ Gamma( k + c, Θ / ( 1+ Θcs) )
- 해당 수식을 반영하여 이전과 동일한 사이즈로 시뮬레이션 데이터를 생성 시킨다.
- Part3. 전환율과 단위 당 수익을 곱하여 예상되는 실제 수익을 계산해본다.
- Part1. 전환율 Simulation 계산 방법
3-2) 기대수익 시뮬레이션 결과 시각화
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
## 시각화를 위한 코드
plt.rcParams['figure.figsize'] = (12, 8)
sns.distplot(control_avg_purchase, label='control')
sns.distplot(treatment_avg_purchase, label='treatment', bins=100)
plt.xlabel('Avg Revenue per Unit')
plt.ylabel('Density')
plt.title('Experiment Posteriors')
plt.grid(alpha = 0.4, linestyle = '--')
plt.legend()
## 베이지안 결과보고
treatment_won = [i <= j for i,j in zip(control_avg_purchase, treatment_avg_purchase)]
chance_to_beat_ctrl = np.mean(treatment_won)
print('P(Control > Treatment): {}%'.format( round( (1-chance_to_beat_ctrl) * 100,2) )
,'P(Control < Treatment): {}%'.format( round( (chance_to_beat_ctrl) * 100,2) )
, sep = '\n'
)
|
cs |
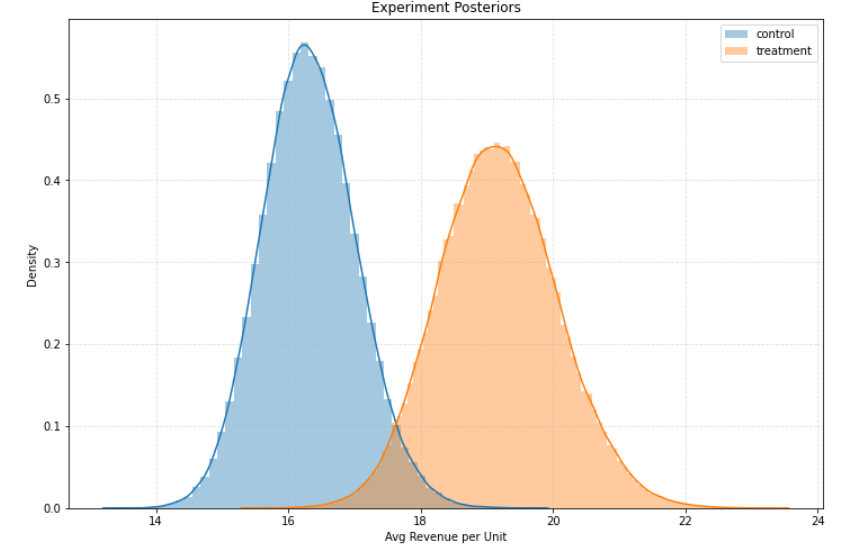
이전 전환율 분포와는 극명하게 다른 양상을 관측할 수 있다. Treatment Group에서 Control보다 전반적인 분포가 우측에 있는 것을 볼 수 있다. 베이지안 확률 결과는 P(Control > Treament) = 0.57%로 계산되었다. 따라서 이 실험에서는 최종적으로 Treatment Group을 선택하는 것이 가장 합리적인 것으로 보인다.
3. 베이지안 결과의 비즈니스 관점 해석
비즈니스 관점에서 가장 중요한 질문은 "그래서 우리는 이 선택을 함으로써 얼마나 수익을 얻고, 어떤 리스크를 회피하는 것인데?"라는 것에 명확한 대답을 할 수 있어야 한다. 이 질문에 대한 대답을 하기 위해서 하나의 노하우를 공유하고자 한다.
- 베이지안 결과를 비즈니스 관점으로 돌려서 해석하기
- 첫 번째. 일주일(예시) 동안 예상되는 단위 산출하기
- 두 번째. 베이지안 기반 전환율
- 세 번째. 베이지안 기반 단위 당 수익
- 네 번째. 기대되는 총 수익을 그룹마다 계산하기
| Group | Sample Size | Conversion Rate | Revenue per Unit | Expected Revnue |
| Treatment | 2,500 | 0.326285 | $ 19.17 | $ 15,625 |
| Control | 2,500 | 0.327396 | $ 16.23 | $ 13,344 |
이렇게 필요한 변수가 모이면 위이 표와 같이 계산할 수 있다. Treatment를 선택하게 되면 일주일에 총 $ 15,625 만큼 수익을 기대할 수 있고, 반대로 Control을 선택하게 되면 동일 기간 $ 13,344 수익을 얻을 수 있다. 만약에 Control을 선택하게 되면 총 $ 2,280만큼 기회비용 리스크가 발생하게 되는 것이다. 따라서 이번 실험 결과를 통해서 약 1만 5천 달러의 수익을 기대할 수 있고, 약 2천 3백 달러만큼의 위험을 회피할 수 있는 성과를 낸 것이다.
'통계학 기초' 카테고리의 다른 글
| [Python] 카이제곱 독립성 검정을 활용한 데이터 분석(feat. A/B Test까지) (0) | 2022.08.30 |
|---|---|
| [Python] COHORT 분석 개념부터 실전 코드까지 (feat. 분석 예제 포함) (0) | 2022.08.18 |
| [Python] 선형회귀분석을 이론, 결과해석, 그리고 코드까지 (Linear Regression Model) (0) | 2022.07.20 |
| [Python] One way ANOVA 분석하기 - 이론부터 코드까지 한 번에 (1) | 2022.06.22 |
| 베이지안 기초4. 실전 A/B Test 코드 구현하기[Python] (0) | 2022.06.07 |



