[글의 목차 - Contents]
1. A/B Test란? - 간단하게 알아보기
2. 베이지안 A/B Test 절차 정리
(1) 기본 데이터셋 설명 - A/B Test의 실전 데이터셋 구현
(2) 베이지안 추론 과정 설계 & Pseudo Code
(3) 실제 코드로 구현하기
(4) 실험 과정 관측 및 실험 결과 해석 하기
1. A/B Test란? - 간단하게 알아보기
A/B Test란 하나의 실험으로서, 원하는 결과(종속변수)를 설정하여 A그룹과 B그룹을 비교해서, 더 높은 결과값을 나타내는 Group을 선택하는 과정을 의미한다.
보통 A/B Test는 기업에서 디자인들의 성과 비교, 클릭률 비교, 전환율 비교 등에 활용되는 용어이자 스킬로서 굉장히 주요한 개념으로 사용한다.
오늘은 베이지안 추론을 활용한 A/B Test에 대해서 100% 실무적으로 어떻게 알고리즘을 구성할 수 있는지 설명해보고자 한다.
해당 포스팅은 이미 베이지안 추론, Python, 기초 통계학을 알고 있다는 가정 하에 최대한 전문적이고 깊게 주제를 다루어볼 예정이다.
또한 이번 학습의 핵심은 단순히 결과만 가지고, stats나 scipy에 나와 있는 파라미터만 채우는 것이 아니라, 실제로 어떻게 학습이 이루어지는지 그 과정을 보면서 알고리즘에 대한 깊은 이해도를 높이는 것이다.
궁극적인 목표는 나의 사이트나 앱에 적용할 수 있는 알고리즘을 구현할 수 있는 능력을 함양하여 실무에 적용할 수 있는 레벨을 달성하는 것이다.
참고로 이 내용은 Udemy의 강의 내용을 기반으로 필자가 재학습한 내용을 정리한 것이다.
원본 강의 링크: URL 참조
2. 베이지안 A/B Test 절차 정리
(1) 기본 데이터셋 설명 - A/B Test의 실전 데이터셋 구현

지금부터 광고 A와 광고 B를 운영하고 있다고 가정하고, 클릭 여부를 0과 1 boolean 값으로 정의한다. 따라서 모든 Row는 impression으로 "고객이 특정 광고를 봤는데, 실제로 클릭했는지 안 했는지"를 표현한 데이터셋이라고 이해하면 된다.
(2) 베이지안 추론 과정 설계 & Pseudo Code
Step1. 베이지안 추론의 정의

베이지안 추론은 Likelihood와 Prior를 갖고, 원하는 Posterior를 추정하는 반복학습의 과정으로 정의할 수 있다. 이를 보다 정확하게 이해하기 위해서는 Conjugate Prior, Naive Bayes Theorm 등의 내용을 공부해보면 이해도를 높일 수 있다.
A/B Test 관점에서 이를 풀어보면, 이전에 갖고 있던 사진 지식(Prior)과 수집한 데이터(Likelihood)를 가지고, 광고 A와 광고 B 중 어떤 것이 실제로 전환율이 더 높은지를 베타 분포에 기반하여 추론하는 것이다.
해당 내용을 이해하기 힘들다면, 이전 포스팅에 베이지안 정리에 대해서 아주 쉽게 시리즈로 정리를 했으니 참고하길 바란다.
Step2. 베이지안 실험의 순서

✅ 베타 분포 - A/B Test 관점에서 쉽게 이해하기
쉽게 말해서 우리는 광고A와 광고B에 대해서 아무런 정보가 없다고 생각하고 실험을 시작하는 것이다. 이것이 가장 현실적인 가정인 이유가 보통은 이전 광고 CTR이 다음 광고 CTR에 그대로 적용된다고 보기에 힘들기 때문이다. 또한 광고를 운영하는 시기와 Trend도 있기 때문에 이번 광고에 대한 모수는 모른다고 가정하는 것이 아니라 실무자들 또한 진짜로 모를 가능성이 농후하다. 따라서 Beta Distribution에서 알파(alpha)와 베타(beta) 값을 각각 1,1로 설정하여 진행하는 것이다.
참고로 베타 분포에서 alpha는 실험에 성공한 횟수를 의미하며, beta는 실패한 횟수를 의미한다. 이를 광고 맥락으로 이해해본다면, alpha는 광고가 클릭된 횟수를 의미하고, beta는 impression만 발생하고 click은 발생하지 않은 경우를 말한다.
- 최종 정리: Beta(alpha, Beta) = Beta Distribution ( 클릭 발생 세션, 전체 Impression 세션 - 전체 클릭 세션 )
✅ 실험 순서 논리 이해하기
첫 번째. 실험 진행하기
첫 번째 단계는 실험 그룹별(광고 그룹)로 학습을 진행하는 것이다. 예를 들어, 아래와 같이 각 Group별로 10회 학습을 했다고 가정해보자
- Group A: 10회 광고 시청 → 3회 클릭 발생 → Beta( 1+3, 1 + (10-3) ) = beta(4, 8)
- Group B: 10회 광고 시청 → 8회 클릭 발생 → Beta( 1+8, 1 + (10-8) ) = beta(9, 3)
Beta분포가 (1,1)로 고정이 아니라 이때까지 수집한 각 10회 데이터를 그룹에 맞게 다시 튜닝시켜주는 순서를 따른다. 쉽게 말해 5회 때 학습한 결과는 계산 당시에는 Posterior로 계산을 했지만, 6회 때 학습을 진행할 때는 Prior 정보로서 사용하는 것이다. 이 부분에 대해서 더 공부를 하고 싶다면 Thompson Sampling을 공부해보고, 이전 포스팅에 개념적인 부분을 설명했으니 참고하기 바란다.
두 번째. Posterior 결과 비교 분석 및 A/B 우승 확률 구하기
이제 순서는 GroupA와 GroupB의 Posterior 결과를 비교하는 것이다. 위의 분포와 비슷한 예시를 만들어 보았다.
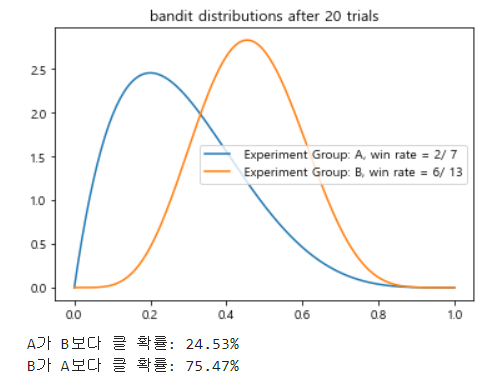
총 20회 학습을 진행했고, 그때 베타 분포는 위와 같이 그려질 수 있다. 이때 A의 Posterior 확률은 2/7= 28%고, B의 Posterior 확률은 6/13 = 46%다. 절대로 실수하면 안 되는 것은 각각의 우승 확률은 위와 같이 Probability Density Function(PDF)을 따르기 때문에 단순이 몇 %p 크다 작다를 비교하는 것이 아니라, 확률적으로 검증이 된 수치인지 판단을 해야 한다.
P(A>B)와 P(B>A)를 이때까지 학습한 샘플의 양만큼 샘플링을 진행한 뒤에 데이터 분포 자체의 비교를 하는 것이다. 만약 분포 자체가 더 크다는 것이 확실하게 판명이 된다면, 결과를 받아들이면 되는 것이다.
연습삼아서 위의 예시로 한 번 베이지안 통계를 해석해보자.
- Group B의 분포가 Group A분포 보다 우측에 위치해 있고, HDI 95%기준으로 봐도 우승 확률이 크다는 것을 알 수 있다.
- P(B > A)는 75.47%로 통계적 검증 기준에는 미치지 못 한다.
- 쉽게 결론을 이해하자면 P(B) - P(A) =18%p이라는 수치가 사실일 가능성이 75.47%이다.
세 번째. Prior 정보 업데이트
위의 예시로 계속 설명을 진행해보겠다. 이제 21번 째 학습을 진행한다고 할 때 Group A가 나왔다고 하자. 이때 질문을 던지자면, A의 베타 분포는 다시 Uniform Distribution - Beta(1,1)으로 시작해야하는가?
그렇지 않고 이전까지 학습한 13회의 학습 데이터를 활용해야 한다. 조금 더 부연 설명을 하자면, 이전까지 20회 학습했을 때 P(A) = 13/20이 될 것이고, 베타 분포는 Beta( 4, 8 ) 이 우리가 알고 있는 Prior로서 활용되는 것이다. 이 정보는 매 학습을 진행해줄 때마다 Impression 및 Click 정보를 담아주면서 자동으로 업데이트될 수 있도록 코드를 구성해볼 예정이다.
(3) 실제 코드로 구현하기
✅ 실험 초기 세팅 - Group별 분포 생성 및 그룹의 선언
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
## (1) BanditA와 BanditB를 선언
class Bandit:
def __init__(self, name):
self.clks = 0
self.views = 0
self.name = name
def add_click(self):
self.clks += 1
def add_view(self):
self.views += 1
# initialize bandits
banditA = Bandit('A')
banditB = Bandit('B')
|
cs |
Bandit은 각 실험 Group이라고 이해하면 된다. 이전 포스팅에서 다루었떤 Slot Machine의 예제 코드를 활용하여 응용한 것이다.
더 중요한 것은 "각 실험 Group을 Class로 정의"하여 옵션이 늘어나도 쉽게 비교 분석할 수 있는 환경을 구축하는 것이다. Bandit이라는 Class를 구축했기 때문에 여기서는 A와 B 두개만 쓰지만, 상황에 따라서 옵션이 A,B,C,D로 늘어나도 추가 코드를 작성하는 것이 아니라 코드 한줄로 선언만 해주면 끝이나게 된다.
초기 세팅 됐을 때는 Impression과 click은 없는 상태이기 때문에 0으로 설정한다. 또한 각 Group마다 실험 정보를 업데이트할 수 있는 기능을 구현하기 위해서 "add_click"과 "add_view"라는 함수를 구성하였다. 이렇게 되면 각 Bandit이 이전까지 몇 번 노출이 발생하였고, 그 중에서 몇 번 클릭이 이루어졌는지 정보를 저장하는 것이다. 이 부분이 바로 Posterior로 알아낸 것을 Prior로 저장하는 부분이다.
✅ 각 실험 진행 시 정보 처리 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
## Part1. Group별 정보 받아오기
bandits = [ banditA, banditB ] sample_points = [9,19,49,100,200,500,1000,1500, 1999]
## Part2. 데이터 사이즈만큼 실험 진행하기 for i in ipb(range(r1.shape[0])):
row_idx = r1.iloc[i]
## A Bandit으로 들어왔을 때
if row_idx.advertisement_id == 'A':
## Bandit A에 View 업데이트
banditA.add_view()
## click 정보 업데이트
if row_idx.action == 1:
banditA.add_click()
## B Bandit으로 들어왔을 때
elif row_idx.advertisement_id == 'B':
## Bandit B에 View 업데이트
banditB.add_view()
if row_idx.action == 1:
banditB.add_click()
else:
print('Input Error: something wrong in {}th row'.format(i))
if i in sample_points:
plot(bandits, i)
## Part3. 실험 결과 요약하기 n_samples = max(bandits[0].views, bandits[1].views)
posterior_A_samples = stats.beta(1 + bandits[0].clks , 1 + bandits[0].views- bandits[0].clks).rvs(n_samples)
posterior_B_samples = stats.beta(1 + bandits[1].clks , 1 + bandits[1].views- bandits[1].clks).rvs(n_samples)
|
cs |
- Part1. Group별 정보 받아오기.
우선 여기서 옵션은 A와 B 두개 이기 때문에 각각의 Class를 선언한다. Sample Points는 어떻게 실험이 돌아가는지 시각화하기 위해서 임의로 설정한 Point들이다. 아래의 시각화 영역에서 활용할 예정이다.
- Part2. 데이터 사이즈만큼 실험 진행하기
for loop을 활용하여, 모든 row에 대해서 학습을 진행하는 반복문을 구성했다. 이때 광고 노출의 Group에 따라 분기처리를 하기 위해서 if문을 활용하였고, 맨 하단의 if 문에서는 어떻게 학습이 진행되고 있는지 보기 위해서 시각화 코드를 넣었다. 해당 시각화 코드는 아래의 영역에서 다룰 예정이다.
- Part3. 실험 결과 요약하기
이 영역은 각 Group 별 CTR을 단순 비교하는 것이 아니라 Probability Density Function(PDF)에 기반하여 확률 분포상 이 차이가 Fact일 확률을 보는 것이다. 직관적으로 말해서 확률 분포 면적 자체를 비교하는 것이다.
이때 초기 세팅이 단일분포를 가정했기 때문에 알파와 베타 값을 1,1로 설정해두고, 클릭이 발생한 세션과 그렇지 못 한 세션을 분포에 반영해준다. 그리고 분포를 그리기 위해서는 샘플링을 진행하게 되는데, 샘플 사이즈는 이때까지 학습했던 integer 중 큰 값을 반영해준다. 이 부분은 빅데이터 환경에서 크게 문제가 되지 않고, 또한 학습 비율도 50 대 50으로 가져가는 것이 convention이기 때문에 편하게 이해하고 넘어가면 된다.
위와 같은 코드로 실험 결과를 비교하게 되면, 실제로 얼마나 데이터에서 차이가 발생하게 되는지 알 수 있다. 실제 결과 해석 방법은 맨 하단에 있으니 참고하길 바란다.
✅ 시각화 코드 및 실험 변화 과정 관측을 위한 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
def plot(bandits, trial):
x = np.linspace(0,1,200)
for b in bandits:
y = stats.beta.pdf(x, b.clks, b.views - b.clks)
plt.plot(x,y
, label = f" Experiment Group: {b.name}, win rate = {b.clks}/ {b.views}"
)
plt.title(f"bandit distributions after {trial + 1} trials")
plt.legend()
plt.show()
# n_samples는 이때까지 학습한 양에 근거해야 함
# 둘 중 학습이 작은 방향으로 하자. 왜냐하면 과대 측정은 실제 데이터 기반이 아니기 때문에
# 또한 사이즈가 커지면 별로 차이가 없기 때문에
n_samples_A = max(bandits[0].views, bandits[1].views)
# 주어진 a와 b 값으로 posterior 분포를 추론한다.
posterior_A = stats.beta(1 + bandits[0].clks , 1 + bandits[0].views- bandits[0].clks)
posterior_B = stats.beta(1 + bandits[1].clks , 1 + bandits[1].views- bandits[1].clks)
posterior_A_samples = posterior_A.rvs(n_samples)
posterior_B_samples = posterior_B.rvs(n_samples)
print('A가 B보다 클 확률: {}%'.format(round((posterior_A_samples > posterior_B_samples).mean()*100 ,2))
, 'B가 A보다 클 확률: {}%'.format(round((posterior_B_samples > posterior_A_samples).mean()*100 ,2))
, sep = '\n')
|
cs |
아까 설정한 sample point들마다 베타 분포가 어떻게 변화하고 있는지 관측하기 위한 코드이다. 각 실험 단계별로 P(B>A)와 P(A>B) 확률 또한 계산하면서 베이지안 통계 추론이 실제로 어떻게 변화하는지 보기 위해서 실험 결과 요약 코드도 포함시켜두었다.
따라서 단순히 얼마나 실험이 진행됐는지 알 수 있을뿐만 아니라, 실험 중간 어떻게 분포가 변화하는지 관찰할 수 있기 때문에 훨씬 더 직관적이고 이해하기 쉬운 A/B Test 시각화를 할 수 있다.
✅ A/B Test 구현을 위한 전체 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
|
## (1) BanditA와 BanditB를 선언 - 𝛼 와 𝛽 는 1,1로 Uniform Distribution
## Author: Byungkuk Ahn class Bandit:
def __init__(self, name):
self.clks = 0
self.views = 0
self.name = name
def add_click(self):
self.clks += 1
def add_view(self):
self.views += 1
# initialize bandits
banditA = Bandit('A')
banditB = Bandit('B')
def plot(bandits, trial):
x = np.linspace(0,1,200)
for b in bandits:
y = stats.beta.pdf(x, b.clks, b.views - b.clks)
plt.plot(x,y
, label = f" Experiment Group: {b.name}, win rate = {b.clks}/ {b.views}"
)
plt.title(f"bandit distributions after {trial + 1} trials")
plt.legend()
plt.show()
# n_samples는 이때까지 학습한 양에 근거해야 함
# 둘 중 학습이 작은 방향으로 하자. 왜냐하면 과대 측정은 실제 데이터 기반이 아니기 때문에
# 또한 사이즈가 커지면 별로 차이가 없기 때문에
n_samples_A = max(bandits[0].views, bandits[1].views)
# 주어진 a와 b 값으로 posterior 분포를 추론한다.
posterior_A = stats.beta(1 + bandits[0].clks , 1 + bandits[0].views- bandits[0].clks)
posterior_B = stats.beta(1 + bandits[1].clks , 1 + bandits[1].views- bandits[1].clks)
posterior_A_samples = posterior_A.rvs(n_samples)
posterior_B_samples = posterior_B.rvs(n_samples)
print('A가 B보다 클 확률: {}%'.format(round((posterior_A_samples > posterior_B_samples).mean()*100 ,2))
, 'B가 A보다 클 확률: {}%'.format(round((posterior_B_samples > posterior_A_samples).mean()*100 ,2))
, sep = '\n')
def experiment():
bandits = [ banditA, banditB ]
sample_points = [9,19,49,100,200,500,1000,1500, 1999]
for i in ipb(range(r1.shape[0])):
row_idx = r1.iloc[i]
## A Bandit으로 들어왔을 때
if row_idx.advertisement_id == 'A':
## Bandit A에 View 업데이트
banditA.add_view()
## click 정보 업데이트
if row_idx.action == 1:
banditA.add_click()
## B Bandit으로 들어왔을 때
elif row_idx.advertisement_id == 'B':
## Bandit B에 View 업데이트
banditB.add_view()
if row_idx.action == 1:
banditB.add_click()
else:
print('Input Error: something wrong in {}th row'.format(i))
if i in sample_points:
plot(bandits, i)
n_samples = max(bandits[0].views, bandits[1].views)
posterior_A_samples = stats.beta(1 + bandits[0].clks , 1 + bandits[0].views- bandits[0].clks).rvs(n_samples)
posterior_B_samples = stats.beta(1 + bandits[1].clks , 1 + bandits[1].views- bandits[1].clks).rvs(n_samples)
# print total reward
print("total reward earned: {}".format(banditA.clks + banditB.clks)
, "overall win rate: {}".format(banditA.clks + banditB.clks / banditA.views + banditB.views )
, '--------------------------'
, 'Group A Result Summary'
, 'Impression: {}, Clicks: {}, CTR: {}%'.format(banditA.views, banditA.clks, banditA.clks / banditA.views*100)
, 'Group B Result Summary'
, 'Impression: {}, Clicks: {}, CTR: {}%'.format(banditB.views, banditB.clks, banditB.clks / banditB.views*100)
, 'Mean Difference: {}'.format( abs(posterior_A_samples.mean() - posterior_B_samples.mean()) *100 ,2)
, 'P-value: {}%'.format(round( (posterior_A_samples > posterior_B_samples).mean()*100 ,2))
, sep = '\n'
)
if __name__ == "__main__":
experiment()
|
cs |
(4) 실험 과정 관측 및 실험 결과 해석 하기
 20회 학습 시 |
 50회 학습 시 |
 100회 학습시 |
 500회 학습 시 |
 1500회 학습 시 |
 |
total reward earned: 676
overall win rate: 0.338
--------------------------
Group A Result Summary
Impression: 1000, Clicks: 304, CTR: 30.4%
Group B Result Summary
Impression: 1000, Clicks: 372, CTR: 37.2%
Mean Difference: 6.77481116104402
P(A>B): 0.1%
베타 분포가 매 실험 단계마다 변화하는 것을 관찰할 수 있다. 100회까지 학습할 때는 A와 B 모두 비슷한 CTR을 보여주었고, 분포또한 비슷한 영역에서 설정되어 있기 때문에 섯불리 누가 Winner 광고라고 판단할 수 없었다.
그러나 500회 이상 학습부터 베타 분포가 자리를 잡으면서 Group B의 PDF가 확실히 우측에 자리를 잡는 것을 알 수 있었고, P(B>A) 또한 80%를 넘어가게 되었다. 2000회 모두 학습을 진행했을 때는 차이가 극명해졌기 때문에 이번 베이지안 A/B Test의 결과는 명확하다고 보인다.
실험 결과를 요약해보면 광고 A의 CTR은 30%이고 광고 B의 CTR은 37%로 약 6.7%p가 났다. 이 확률이 거짓일 확률은 0.1%로 진실이라고 받아들어야 한다. 따라서 광고 운영에 있어서 앞으로는 광고 B를 전체 노출시키는 것으로 판단해야 데이터에 기반한 의사결정일 것이다.
'통계학 기초' 카테고리의 다른 글
| [Python] 선형회귀분석을 이론, 결과해석, 그리고 코드까지 (Linear Regression Model) (0) | 2022.07.20 |
|---|---|
| [Python] One way ANOVA 분석하기 - 이론부터 코드까지 한 번에 (1) | 2022.06.22 |
| 베이지안 기초3. 베이지안을 활용한 A/B Test 예시[Python] (0) | 2022.04.26 |
| 베이지안 기초2. 베이지안 Classification의 이해 (0) | 2022.04.15 |
| 베이지안 기초1. 기초 개념 및 예시를 통한 완벽 이해 (0) | 2022.04.07 |



