1. 재귀함수의 기본 원리
2. 재귀함수의 기본 문제 연습 - 피보나치 수열
1. 재귀함수의 기본 원리
(1) 재귀함수의 정의
: 함수 안에 자신의 함수를 다시 호출하는 함수를 의미합니다. 이러한 재귀함수는 자신의 로직을 내부적으로 반복하다가, 일정한 조건이 만족되면 함수를 이탈하여 결과를 도출합니다.
(2) 재귀함수의 기본적인 구현 방법 2가지
일반적으로 재귀함수는 2가지 형태로 표현될 수 있습니다.
우선 기본적인 표현식을 익히고, 간단한 예시를 통해서 그 원리를 이해해보도록 하겠습니다.
1) 첫 번째 재귀함수 표현 방법
|
1
2
3
4
5
|
def function(입력):
if 입력 > 일정값: # 입력이 일정 값 이상이면
return function(입력 - 1) # 입력보다 작은 값
else:
return 일정값, 입력값, 또는 특정값 # 재귀 호출 종료
|
cs |
첫 번째 방법은 재귀함수를 호출하는 부분을 상단에 두고 표현할 수 있다는 것입니다. 첫 번째 if 문에서 보실 수 있듯이, 일정한 조건을 만족하지 않으면, 계속해서 자기 자신의 함수로 되돌리는 코드를 볼 수 있습니다.
이때 " - 1"은 하나의 예시일 뿐 감소하는 패턴은 여러가지가 될 수 있습니다.
2) 두 번째 재귀함수 표현 방법
|
1
2
3
4
5
|
def function(입력):
if 입력 <= 일정값: # 입력이 일정 값보다 작으면
return 일정값, 입력값, 또는 특정값 # 재귀 호출 종료
function(입력보다 작은 값)
return 결과값
|
cs |
두 번째 방법은 재귀함수가 돌아가는 부분은 아래의 부분에 삽입하는 것입니다. 위의 방법은 재귀함수가 돌아가는 부분이 상단 조건에 삽입되어있던 것을 비교해서 보면 확실히 다른 것을 알 수 있겠죠.
두 방법 모두 유효한 방법이고, 상황에 따라 필요한 코딩이 달라질 수 있으니 두 방법 다 익숙해지도록 연습하는 것이 중요할 것입니다.
3) 팩토리얼을 통한 재귀함수 표현법 연습
팩토리얼은 많이들 들어보셨을 것이라 생각합니다. 쉽게 말해서 5!이면 5 x 4 x 3 x 2 x 1로 표현될 수 있습니다. 정답은 120이 되겠죠. 이것을 한 번 재귀함수로 표현해보도록 하겠습니다.
- 첫 번째 방법을 통한 재귀함수 표현
|
1
2
3
4
5
6
|
def factorial(x):
if x > 1:
return x * factorial(x - 1)
else:
return x
|
cs |
그러면 1부터 10까지 팩토리얼을 적용하여 결과가 잘 도출되는지 한 번 확인해보도록 하겠습니다.

- 두 번째 방법을 통한 재귀함수 표현
두 번째 방법처럼 상단에 재귀함수 조건을 조건이 있는 함수를 만들어 보았습니다.
|
1
2
3
4
5
|
def factorial2(num):
if num > 1:
return num * factorial2(num-1)
return num
|
cs |
이 함수를 이용하여 첫 번째 예시와 동일하게 결과를 찍어보도록 하겠습니다.
만약 이 조건이 틀렸다면, 다른 결과를 호출할 것이고, 내부의 논리가 동일하면 그 결과 또한 똑같을 것입니다.
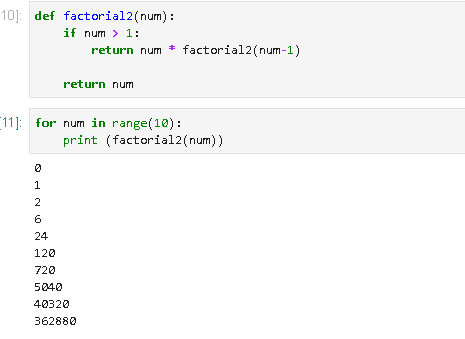
첫 번째 구현한 팩토리얼과 정확하게 동일한 결과 값을 호출한 모습을 볼 수 있습니다.
따라서 재귀함수는 상단 혹은 하단에 자기 자신을 호출하는 방법을 모두 알고 있으면 다양하게 활용할 수 있는 것을 확인하였습니다.
2. 재귀함수의 기본 문제 연습 - 피보나치 수열
피보나치 수열은 자신의 인자 앞 두개를 계속해서 더해 나가는 수열을 의미합니다.
피보나치 수열에 대해서는 아래의 링크로 설명을 대체하도록 하겠습니다. 개인적으로 통계나 이과 출신이시라면 정말 지겹도록 들어봤던 수열이라고 생각합니다.
(출처: ko.wikipedia.org/wiki/%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98_%EC%88%98)
이를 재귀함수로 표현하게 된다면 아래의 코드처럼 구현할 수 있습니다.
|
1
2
3
4
5
6
|
def fibo(n):
if n <= 1:
return n
else:
return fibo(n-1) + fibo(n-2)
|
cs |
앞에서 보시다시피 n이 1이 되기 이전까지 지속적으로 피보나치 함수를 재귀적으로 호출하여 계산하는 것을 볼 수가 있죠.
이를 통해 실제 계산된 피보나치 수열의 결과를 살펴보도록 합시다.

피보나치 수열의 시작이 1이라고 가정했을 때, 다음과 같이 표현될 수 있습니다. 이런 식으로 각 항의 값들을 모두 계산할 수 있고, 원한다면 특정 숫자의 피보나치 값을 찾아낼 수 있겠죠.
이로서 재귀함수의 모든 기본적인 표현 방법을 알아봤습니다. 재귀함수는 이후 포스팅할 고급 정렬, 동적 계획법 등에서도 지속적으로 나올 예정입니다.
그러니 재귀함수만큼은 원리부터 코드 구현까지 반드시 숙지하고 있어야할 chapter라고 생각합니다.
'Python > 알고리즘' 카테고리의 다른 글
| 고급정렬2. 퀵정렬(Quick Sort) 완벽 마스터하기 (0) | 2021.01.06 |
|---|---|
| 고급정렬1. 병합정렬(Merge Sort) 완벽 마스터하기 (0) | 2021.01.04 |
| 동적 계획법(DP)과 분할 정복 마스터하기 (0) | 2021.01.01 |
| 기본 정렬3. 선택 정렬(Selection Sort) 구현하기 (0) | 2020.12.30 |
| 기본 정렬2. 삽입 정렬(Insertion Sort) (0) | 2020.12.29 |


