1. 병합 정렬(Merge Sort)이란?
2. 병합정렬의 예시 및 원리 이해
3. 병합 정렬의 코드 구현
1. 병합 정렬(Merge Sort)이란?
(1) 병합 정렬의 개념
1) 병합 정렬은 "재귀함수"를 이용한 정렬 알고리즘입니다.
2) 병합 정렬의 순서
- 데이터를 반으로 분리한다.
- 데이터의 길이가 1이 될 때까지 계속 반복적으로 분리하다. (재귀함수를 이용)
- 갈라진 리스트를 병합할 때, 순서에 맞게 정렬하여 병합한다.
이 원리를 이미지로 쉽게 이해해보면 아래의 그림과 같습니다. 이미지 원본 링크

설명만으로는 바로 이해하기 쉽지 않기 때문에 한 번 예시를 통해서 원리를 다시 한 번 이해해보도록 하겠습니다.
2. 병합정렬의 예시 및 원리 이해
(1) 예시 데이터: [1, 9, 3, 2]
1) 나누는 프로세스
첫 번째. [1, 9]와 [3, 2]로 나눕니다.
두 번째. [1]과 [9]로 또 나누고, [3]과 [2]로 나눕니다. 결과론적으로 1 / 9 / 3 / 2 로 세분화가 완료되었습니다.
2) 병합하는 프로세스
첫 번째. 1과 9를 비교했을 때, 1 <9 이기 때문에 [1, 9]로 만들어 줍니다.
두 번째. 3과 2를 비교했을 때, 2< 3 이기 때문에 [2, 3]으로 만들어 줍니다.
세 번째. [1, 9]와 [2, 3]을 비교하여, 작은 순서대로 재정렬을 합니다. 결과적으로 [1, 2 ,3 ,9]로 만들어줍니다.
(2) 원리의 이해
병합 정렬을 구현하기 위해서는 총 두 가지의 함수가 필요하다는 것을 알았습니다. 하나는 데이터를 쪼개는 함수와 다른 하나는 데이터를 병합하는 함수이죠.
데이터를 쪼개는 함수에서 포인트는 재귀용법을 통한 데이터의 완벽한 분리이고, 데이터를 병합하는 함수에서는 정확한 크기 비교를 위한 케이스별 데이터 처리가 될 것 같습니다.
3. 병합 정렬의 코드 구현
(1) 병합 정렬의 손 코드 계획 구성
1) 데이터를 나누는 함수: merge_split(data)
- 만약 리스트 갯수가 한개이면 해당 값 리턴
- 그렇지 않으면, 리스트를 앞뒤, 두 개로 나누기
- left = mergesplit(앞)
- right = mergesplit(뒤)
- merge(left, right) -> 합치는 것이 최종 목표이기에
2) 데이터를 합치는 함수: merge(왼쪽, 오른쪽)
- 리스트 변수 하나 만들기 (sorted)
- left_index, right_index = 0
- while left_index < len(left) or right_index < len(right):
- 만약 left_index 나 right_index 가 이미 left 또는 right 리스트를 다 순회했다면, 그 반대쪽 데이터를 그대로 넣고, 해당 인덱스 1 증가
- if left[left_index] < right[right_index]:
- sorted.append(left[left_index])
- left_index += 1
- else:
- sorted.append(right[right_index])
- right_index += 1
(2) 병합 정렬의 실제 코드 구현
1) merge_split(data)의 구현
|
1
2
3
4
5
6
7
8
9
|
def merge_split(data):
if len(data) <= 1:
return(data)
else:
medium = round(len(data)/2)
left = data[:medium]
right = data[medium:]
return split(left), split(right)
|
cs |
주의하실 점은 맨 마지막 return에서 왼쪽 오른쪽을 계속 나누는 것을 보여준 것은 실제로 데이터까 쪼개지는 것을 구현하기 위함입니다.
저희의 목적은 데이터를 병합하는 것이기 때문에 나중에는 저 부분이 병합하는 함수로 대체될 예정입니다.

난수로 10개의 정수를 생성하여, 한번잘게잘게 쪼개보았습니다. 아주 잘 쪼개진 모습을 볼 수 있습니다.
2) merge 함수의 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
def merge(left,right):
merged = list()
lpoint, rpoint = 0,0
## case1 왼쪽 오른쪽 남아있을 때
while len(left) > lpoint and len(right) > rpoint:
if left[lpoint] > right[rpoint]:
merged.append(right[rpoint])
rpoint += 1
else:
merged.append(left[lpoint])
lpoint += 1
## case2 왼쪽 데이터만 남아있을 때
while len(left) > lpoint:
merged.append(left[lpoint])
lpoint += 1
## case3 오른쪽 데이터만 남아있을 때
while len(right) > rpoint:
merged.append(right[rpoint])
rpoint += 1
return merged
|
cs |
이번에는 병합하는 함수인데요, 여기서의 포인트는 인덱싱 방법과 케이스별 정리입니다. 왼쪽 오른쪽을 비교할 때 순차적으로 비교하기 위해서 왼쪽 위치(lpoint)와 오른쪽 위치(rpoint)를 지정해주고, 모든 경우의 수를 비교할 수 있게 준비를 했습니다.
비교를 할 때 왼쪽 오른쪽 모두 데이터가 있는 경우가 있고, 오직 왼쪽 데이터만 남아있는 경우가 있고, 마지막으로 오른쪽 데이터만 남아있는 경우가 있겠죠. 그래서 Case를 주석에서 보시다시피 3가지로 나누었습니다.
그래서 비교가 끝난 이후에는 indexing 정리를 위해서 각 point에 1을 더해준 것입니다.
3) 최종 코드 및 구현 결과
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
def merge(left,right):
merged = list()
lpoint, rpoint = 0,0
## case1 왼쪽 오른쪽 남아있을 때
while len(left) > lpoint and len(right) > rpoint:
if left[lpoint] > right[rpoint]:
merged.append(right[rpoint])
rpoint += 1
else:
merged.append(left[lpoint])
lpoint += 1
## case2 왼쪽 데이터만 남아있을 때
while len(left) > lpoint:
merged.append(left[lpoint])
lpoint += 1
## case3 오른쪽 데이터만 남아있을 때
while len(right) > rpoint:
merged.append(right[rpoint])
rpoint += 1
return merged
def merge_split(data):
if len(data) <= 1:
return data
else:
medium = round(len(data)/2)
left = merge_split(data[:medium])
right = merge_split(data[medium:])
return merge(left, right)
|
cs |
위에서 가장 주의할 점은 맨 마지막에 merge(left, right)로 제가 수정했습니다. 처음에 보여드릴 때는 잘게 잘게 쪼개진 것을 보여드렸는데, 그것은 이해를 돕기 위함이었고 실제로는 데이터를 합쳐야하기 때문에 merge함수를 삽입했습니다.
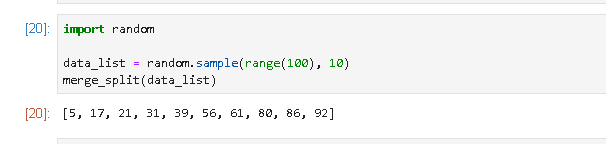
네 난수 10개가 아주 정확히 정렬된 모습을 보실 수 있습니다.
여기까지 병합 정렬에 대한 설명이었습니다. 보시다가 이해가 안 되시는 부분은 항상 댓글로 남겨주시면 최대한 답변을 드디로독 하겠습니다!!
'Python > 알고리즘' 카테고리의 다른 글
| 탐색 알고리즘 - 순차 탐색(Sequential Search) (0) | 2021.01.09 |
|---|---|
| 고급정렬2. 퀵정렬(Quick Sort) 완벽 마스터하기 (0) | 2021.01.06 |
| 동적 계획법(DP)과 분할 정복 마스터하기 (0) | 2021.01.01 |
| 재귀함수의 완벽 이해 및 구현(Recursive Function) (0) | 2020.12.31 |
| 기본 정렬3. 선택 정렬(Selection Sort) 구현하기 (0) | 2020.12.30 |

