1. 활용 데이터셋
이전에 통계학에서 다루는 대표적인 상관 관계분석 모델을 이전 포스팅에서 알아봤다. 이번에는 실습을 해볼 차례로, 와인 데이터셋을 활용할 것이다. 이 데이터셋은 데이터 입문자들에게 아주 유용한 자료이니 비단 이 자료만이 아니더라도 활용해볼만한 가치가 있다고 생각한다.
https://www.kaggle.com/datasets/yasserh/wine-quality-dataset?select=WineQT.csv
Wine Quality Dataset
Wine Quality Prediction - Classification Prediction
www.kaggle.com

여기서는 총 13가지 Column들이 있는데, 실제 의미를 따지기 보다는 모델 실급에 적한한 변수들을 취사선택하여 실제 모델 해석하는 연습에 초점을 둘 것이다.
※ Column들의 정보 정리
| 1 - fixed acidity (결합산) 2 - volatile acidity 3 - citric acid 4 - residual sugar 5 - chlorides 6 - free sulfur dioxide |
7 - total sulfur dioxide 8 - density 9 - pH 10 - sulphates 11 - alcohol Output variable (based on sensory data) 12 - quality (score between 0 and 10) |
(사실 저도 와알못이라 결합산, 유동산 등이 뭔지 모르고, 잔여당이 와인 품질에 어떤 영향력을 갖는지 이론적으로 1도 모릅니다... 그래서 그냥 모델링 연습용도)
2. 상관관계 분석을 위한 EDA
(1) 단일 변수 분포 파악 - Shaprio와 Skewness 측정을 통한 변수의 분류
1) Shapiro 모델을 통한 정규성 검정
Shaprio(샤피로) 모델은 변수가 정규 분포의 형태를 보이는지 아닌지 검증해주는 모델이다.
H0: 변수의 분포는 정규 분포를 만족한다.
H1: 변수의 분포는 정규 분포를 만족하지 않는다.
2) Skewness 측정을 통한 변수 분류
왜도(Skewness)는 절대값이 3 미만일 때 크게 문제 삼지 않는 것이 추세 [1]이긴하다. 예를 들어, 왜도의 절대값이 2인 경우 Shapiro 모델상 정규 분포 결과는 나오지 않지만, 왜도가 크게 뒤틀렸다고 보지 않기 때문에 모델을 돌려도 적합하다는 판단을 내릴 수 있다.
✅ Best Distribution: Shapiro 모델 H0 채택 & Skewness == 1
✅ Practical Distribution: | Skewness | < 3

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
variable_list = r1.columns
## 피어슨 대상 분석
pearson_variable = []
## 이외 모델 대상 분석
other_variable = []
for i in ipb(range(r1.shape[1])):
variable_name = variable_list[i]
variable = r1.iloc[:, i]
## 정규성 검정
## H0: 변수의 분포는 정규분포를 만족한다 VS H1: 변수의 분포는 정규분포를 만족하지 않는다.
shapiro_test = stats.shapiro(variable)
## p-value 0.05 이하라는 것은 귀무가설을 기각하고, 대체가설을 채택하는 것. 따라서 정규분포가 아니다.
## 다만 이런 이상적인 경우는 거의 없으니 왜도 측정을 통한 변수 분류를 한다.
if shapiro_test[1] <= 0.05:
## 왜도 - 절대값 2 이내면 okay to go
if abs(stats.skew( variable, bias = False) ) <= 2:
pearson_variable.append(variable_name)
print('{}변수는 shaprio모델 결과 정규 분포를 만족하지 않습니다.(pvalue = {})'.format(var_name, round(shapiro_test[1], 2))
, '하지만 skewness가 {}임으로, 상관관계 분석을 진행 가능 추정'.format(abs(stats.skew( variable , bias = False) ))
, '===================='
, sep = '\n')
else:
other_variable.append(variable_name)
print('{}변수는 shaprio모델 결과 정규 분포를 만족하지 않습니다.(pvalue = {})'.format(var_name, round(shapiro_test[1], 2))
, '또한 skewness가 {}임으로, 피어슨 모델은 채택하지 않습니다.'.format(abs(stats.skew(variable , bias = False) ))
, '===================='
, sep = '\n')
else:
pearson_variable.append(variable_name)
print('{}변수는 shaprio모델 결과 정규 분포를 만족합니다.(pvalue = {})'.format(var_name, round(shapiro_test[1], 2))
, '===================='
, sep = '\n')
|
cs |
 |
 |
모델 결과 Pearson Correlation Analysis에 적합한 변수는 총 10개이다. 다만, id 변수 같은 경우 변수보다는 identifier에 가깝기 때문에 분석에서 제외한다.
(2) 변수 간 선형 관계 파악 - Seaborn Pair Plot
Pair Plot은 변수 간 선형 관계가 있는지 알아 볼 수 있는 함수로 상관 관계를 찾을 때 굉장히 유용한 시각화 방법이다. 시각화 방법에 따라 정사각형 혹은 삼각형 형태로 할 수 있는데, 개인적으로 삼각형 형태를 선호한다.
 |
 |
Pair Plot의 장점
- 모든 변수 간 상관 관계를 검증할 필요가 없다. 만약 실행했다면, nC2 이기 때문에 이 경우 9*8 / 2 = 36가지 Case를 검증해야 한다. 물론 for loop로 해버리면 그만이긴 하지만, 원론적으로 비효율적인 방법이라고 생각한다.
- 특정 변수에서 관심있는 것을 선택하여 분석할 수 있다. 위의 경우 뚜렷한 양 & 음의 상관 관계에 있는 변수들을 뚜렷하게 관찰할 수 있다.
→ 양의 상관관계 변수 목록
- Density & Fixed Acidity
- Citric Acid & Fixed Acidity
→ 음의 상관관계 변수 목록
- Ph & Fixed Acidity
- Density & Alcohol
(3) 스피어만 & 켄달타우 분석용 변수 목록
위에서 왜도와 Shapiro 결과에서 탈락한 변수들은 스피어만과 켄달 타우 분석 연습 변수로 사용하도록 한다.

3. 상관관계 분석
(1) 피어슨 상관관계 분석 ( Pearson Correlation Analysis )
1) 중요 변수의 Pearson Correlation Test
- 모든 변수 간 상관관계 계수의 측정
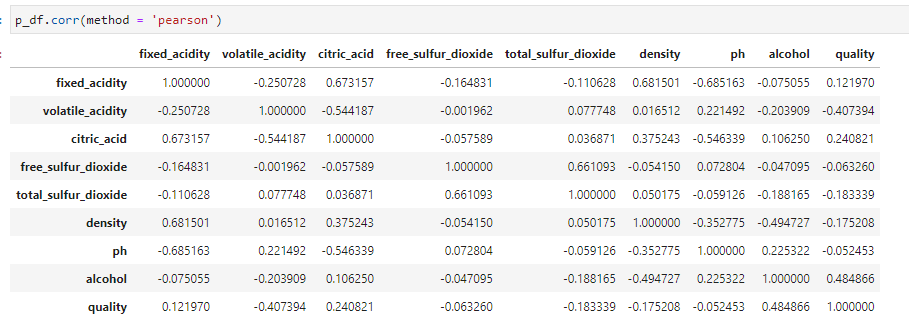
모든 변수 간 상관관계 계수를 측정하려면 위와 같은 메소드를 쓰면 간단하게 실행할 수 있다. 다만, 여기서는 p-value를 볼 수 없기 때문에 검증된 숫자라고 보기 힘들다.
- 중요 변수 간 상관관계 검증
 |
 |
위에서 검증하기로 한 변수들은 역시나 p-value가 검증된 것을 볼 수 있다. 이와 같은 방식으로 가장 효율적이고 효과적으로 상관관계 분석을 진행할 수 있는 것이다.
- 상관계수 해석 방법
| 상관계수 범위 (절대값 기준) | 해석의 방법 |
| r ≥ 0.8 | 강한 상관 관계가 있다. |
| 0.6 ≤ r <0.8 | 상관 관계가 있다 |
| 0.4 ≤ r <0.6 | 약한 상관관계가 있다 |
| r <0.4 | 상관관계가 거의 없다. |
→ 양의 상관관계 결과 및 해석
- Density & Fixed Acidity: 0.68 → + 상관관계가 있다.
- Citric Acid & Fixed Acidity: 0.67 → +상관관계가 있다.
→ 음의 상관관계 변수 목록
- Ph & Fixed Acidity: -0.68 → - 상관관계가 있다.
- Density & Alcohol: -0.49 → 약한 - 상관관계가 있다.
2) Heatmap을 통한 상관관계의 시각화
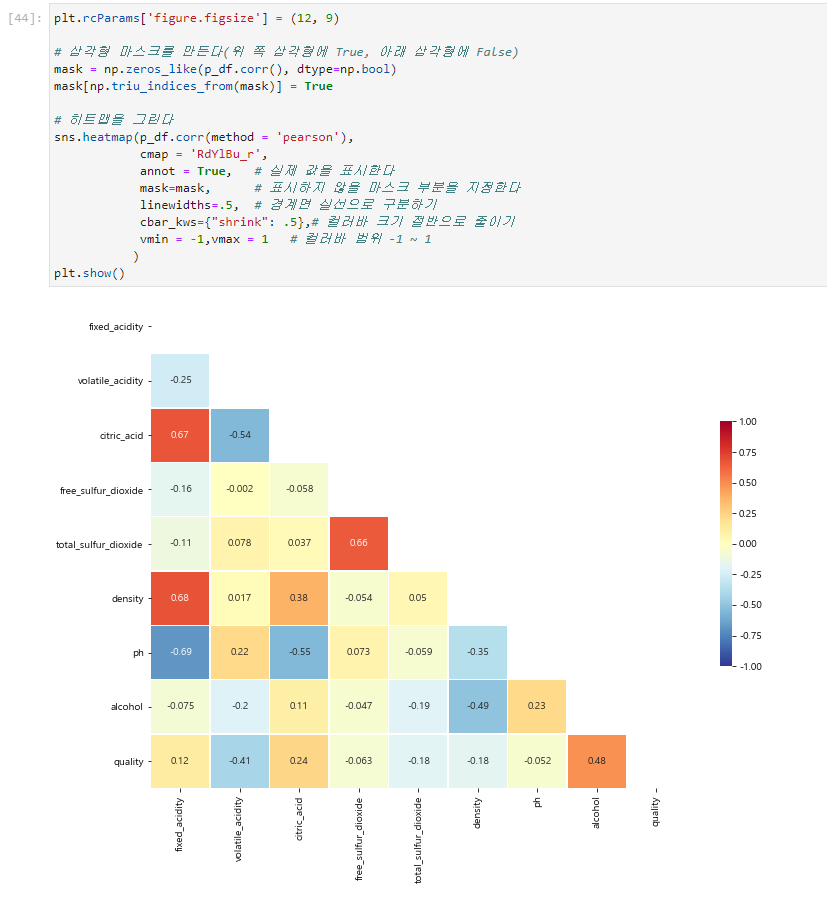
단순히 숫자만 보여주면 일반인들을 대상으로 커뮤니케이션할 때 비효율적인 면이 있다. 따라서 효과적인 모델 검증 결과를 가장 최적화하여 보여줄 수 있는 Heatmap을 사용해보도록 하자.
(2) 스피어만 상관관계 분석 ( Spearman Correlation Analysis )
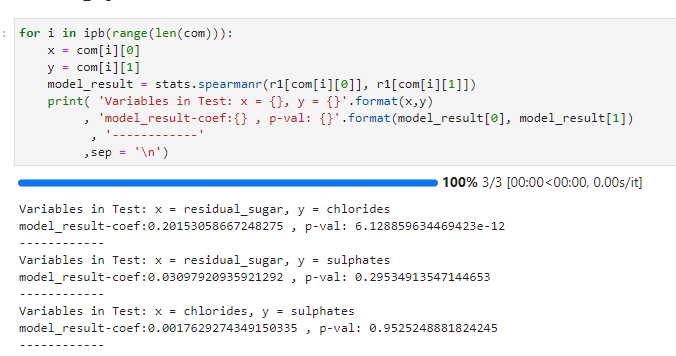
(3) 켄달타우 상관관계 분석 ( Kendall Correlation Analysis )
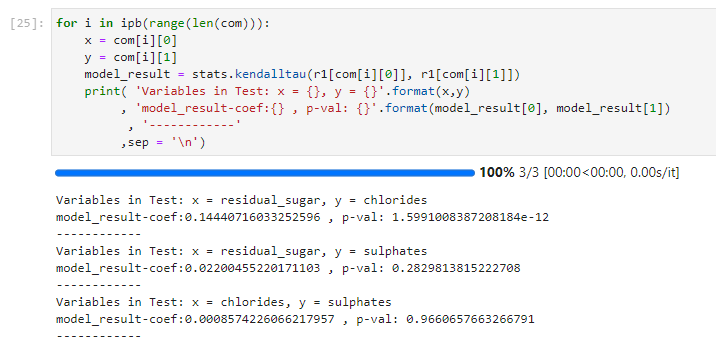
번외로 실시한 스피어만과 켄달타우 상관관계분석에서 유의하게 나온 변수는 Residual Sugar와 Cholrides이다. 다른 변수는 스피어만과 켄달타우 모두 유의하게 나왔다. 따라서 상호 상관관계가 있다고 볼 수 있을 것이다.
4. 분석의 결론
Lesson 1. 변수의 특성에 따라 어떤 상관관계 모델을 선택하는지 이론적 학습
Lesson 2. 각 변수에 적절한 사전 검증 방법 실습
Lesson 3. 효율적인 모델 변수 선정 및 시각화 방법 적용 연습
Reference
- [1] West, S. G., Finch, J. F., & Curran, P. J. (1995). Structural equation models with nonnormal variables: Problems and remedies. In R. H. Hoyle (Ed.), Structural equation modeling: Concepts, issues, and applications (p. 56–75). Sage Publications, Inc.
'통계학 기초' 카테고리의 다른 글
| 베이지안 기초4. 실전 A/B Test 코드 구현하기[Python] (0) | 2022.06.07 |
|---|---|
| 베이지안 기초3. 베이지안을 활용한 A/B Test 예시[Python] (0) | 2022.04.26 |
| 베이지안 기초2. 베이지안 Classification의 이해 (0) | 2022.04.15 |
| 베이지안 기초1. 기초 개념 및 예시를 통한 완벽 이해 (0) | 2022.04.07 |
| 상관관계 분석의 기초 정립 [Python 활용] (0) | 2022.03.30 |



