CUPED란 Controlled Experiments by Utilizing Pre-Experiment Data의 약자로, 온라인 환경에서 A/B Test를 진행할 때 빈도주의 모델 성능을 획기적으로 개선시켜 줄 수 있는 모델을 의미한다. 이번 포스팅에서는 CUPED의 통계적 이론부터 시작하여, Python을 기반으로 어떻게 구현할 수 있는지에 대해서 다루어보고자 한다.
목차
1. CUPED 논문 소개
2. 사전 지식 익히기 - A/B Testing & 독립표본 T-Test
3. 사전 지식 익히기 - 기존 빈도주의 모델의 한계
4. CUPED 이론 이해하기
5. CUPED 코드로 구현하기
1. CUPED 논문 소개
CUPED는 Controlled Experiments by Utilizing Pre-Experiment Data로, 기존 A/B Testing의 성능을 완전히 업그레이드할 수 있는 모델을 의미한다. 이 방법은 2013년 Microsoft에서 최초로 개발되었으며, 현재는 넷플릭스, 페이스북 등 A/B Test를 진행하는 거의 모든 회사에서 채택하고 있는 아주 유명한 모델이다.

아주 쉽게 말해서 CUPED는 기존의 T-Test를 활용한 A/B Test의 한계점을 극복하는데 초점을 두었다. 기존 T-Test의 한계는 변동성(Variation)에 취약할 수밖에 없는 약점을 갖는데, CUPED는 이 단점을 극복하는 방법으로 실험 이전의 데이터를 활용하여 보다 빨리 그리고 적은 데이터만 갖고도 A/B Test에서 우승자를 선정할 수 있게 하는 장점을 지니고 있다.
이번 포스팅에서는 전통적인 빈도주의 모델링(T-Test)과 한계점을 다루어보고, CUPED는 어떻게 이것을 사전 데이터로 극복했는지 자세히 다루어보고자 한다. 나아가 Python 기반으로 코드까지 구현하여 최대한 자신의 환경에 맞게 튜닝하여 쓸 수 있도록 제시하는 것을 목표로 두었다.
2. 사전 지식 익히기 - 독립표본 T-Test 및 한계점
📓전통적인 A/B Test의 방법론 - 독립표본 T 검정에 대한 소개
A/B Test에서 가장 흔하게 쓰는 빈도주의 방법론은 바로 독립표본 T-Test다. 두 개의 집단이 평균에 차이가 있는지 없는지를 밝혀내는 간단한 모델링이다. ( 독립표본 T-Test의 자세한 설명 )
이 모델링에서 가장 중요한 것은 두 가지 Point이다. 첫 번째는 모델의 Effect Size이고 두 번째는 P-value를 확인하는 것이다. Effect Size는 아주 쉽게 말해서 집단 간 평균 차이가 얼마큼 나는지 측정하는 것으로, T-Test에서는 대표적으로 T-Statistics를 통해서 확인한다. P-value를 아주 쉽게 말해보면, 이 분석 결과가 틀릴 확률이 얼마나 될까를 숫자로 표현한 것이다. 보통 사회과학에서는 0.05를 기준으로 모델의 결과가 유의한 지 안 한지 판단한다. P-value의 특징 중 하나는 본질적으로 Sample Size(n)과 변동성(Variance)에 영향을 받을 수밖에 없다는 것이다. 따라서 확실한 결과를 산출하기 위해서는 어떻게 해서든 변동성을 줄여서 일정한 P-value를 도출하는 것이 핵심인 것이다.

🔎 Effect Size와 P-value는 어떻게 이해하면 되나요?
- Effect Size는 T-Statistic 중 Signal에 해당하고, 평균차이가 얼마나 많이 나는가를 보여주는 지표입니다.
- P-Value는 평균 차이가 얼마나 확실한지, 오류의 확률(제1종 오류를 범할 확률)은 없는지 보여주는 대표적인 지표입니다.
- T-Test에서 말하는 Signal to Noise 비율은 평균 차이 대비 얼마나 안정적인 결과를 보여주는지 판단하는 개념입니다. 동일한 Signal이어도, Noise의 비율이 적으면 T-statistics는 커질 수 있다는 것을 알 수 있습니다.
❗T-Test 빈도주의의 한계점
기존에는 모델에서 가장 취약점은 바로 Noise에 해당하는 변동성에 굉장히 취약하다는 점이다. 각 Group의 표준편차가 처지게 되면 자연스럽게 분모값이 커지기 때문에 T-statisics가 감소하게 되며, 그 결과 또한 불안정적으로 변하게 된다. 본질적으로 Variant(분산, 표준편차)가 커지게 되면 일정한 결과를 산출하기가 힘들어지고, 데이터를 더 많이 모아야 하는 문제가 발생한다. 설명만으로는 이해하기 어려울 수 있기 때문에 간단한 예시를 들어보겠다.
Variance가 클 때 모델 결과 및 확률 |
Variance가 작을 때 모델 결과 및 확률 |
✅ 간단한 예시 - 동일한 평균이라도, 분산(Variance)에 따라 실험 결과는 바뀔 수 있어요.
- 무슨 상황일까요?
: Group A의 평균은 10이고, Group B의 평균은 7입니다. 이때 분산이 변하는 것에 따라서 실험 결과가 어떻게 바뀌는지 관찰해 봅시다. - 왼쪽 그래프 - 분산이 큰 경우 볼 수 있는 그래프입니다. 여기서 Group A가 Group B를 이길 확률(P-value)은 60% 밖에 지나지 않습니다. 1종 오류를 피하려면 P-value가 5% 이하가 나와야 하는데 이에 미치지 않습니다.
- 오른쪽 그래프 - 분산이 작은 경우 볼 수 있는 그래프입니다. Group A가 Group B를 이길 확률이 4%가 나옵니다. 분산을 줄이고 안정적으로 만들면 실험 결과가 이렇게 달라질 수 있습니다.
따라서 T-Test의 한계점을 한 줄로 요약하면, 분산과 표본 사이즈에 크게 영향을 받을 수밖에 없는 구조이기 때문에 분산을 줄일 수 있는 방법이 있다면 실행해야 한다는 것이다.
4. CUPED 이론 이해하기
CUPED의 목표는 T-Test의 Signal to Noise Ratio 중에서 Noise에 해당하는 변동성을 줄이는 것이다. 이 목표를 달성하기 위해 CUPED 모델에서는 동일한 지표를 검증할 때, 실험 이전 데이터와 실험 이후 데이터를 같이 학습한다. 이게 왜 가능한지 논문에 나와 있는 수식을 소개하도록 하겠다.
🔎 CUPED의 통계적 원리 - 우리가 최소화시켜야 하는 변수를 찾아보자
- Step1. T-Test의 논리를 알아보자
- T-Test는 Noise에 해당하는 평균 차이들의 변동성을 줄여야 하는 것이 목표이다.
- Step2. 최소화 시켜야 하는 변수는 분모에 해당하는 변동성
- 두 집단 간 차이의 변동성을 최소화시켜야 우리는 결국 signal to noise, T 검정 값을 최대화시킬 수 있는 것이다.
- Step3. 우리는 앞으로 변동 값을 델타(Δ)라고 생각해보자
- 결국에는 두 집단 간 평균 차이에 해당하는 Δ을 최소화 시키면 모델링의 목표를 달성할 수 있는 것이다.

여기서 핵심적으로 알 수 있는 것은 우리의 최종 변수 Delta는 두 개의 변수에 의해서 좌우된다. 한 가지는 Treatment의 종속변수(Yt) 값이고 또 다른 하나는 Control Group의 종속변수(Yc)이다. 그렇다면 자연스럽게 각 변수의 표준편차를 줄일 수 있는 방법을 찾으면 Delta의 Variance까지 감소하는 것을 기대할 수 있을 것이다.
🔎 개별 Y값에 대해서 어떻게 하면 변동성(분산, 표준편차)을 줄여볼 수 있을까?
여기서부터 CUPED의 마법이 들어가는데, 바로 우리의 종속변수와 상관이 없는 다른 변수 X를 가정하는 것이다. CUPED에서는 이 X를 실험 이전의 데이터로 산정하여 개별 Y Treatment와 Y Control의 개별적인 변동성을 줄이는 것이다. 왜 완전 독립적인 변수 X가 변동성을 감소시킬 수 있는지에 대해서 간략하게 소개해보겠다.

- Step1. 완전히 독립적인 변수 X를 삽입한 이유
- 우리의 변수 Y의 평균 좌우 양변에 완전히 독립적인 변수 X의 평균을 더했다고 가정해 보자. 여기서 초기 theta θ 값은 아직 알 수 없는 상태이다.
- Step2. 양변의 분산(Variance)을 계산
- 여기서 변동성을 최소화시키려면, X 변수가 포함된 값이 0이면 된다. 이것을 가능하게 하는 가장 이상적인 θ값을 rho ρ라고 해보자.
- Step3. ρ값을 찾았을 때, Y의 분산
- 우리는 이상적인 값을 찾았을 때 ρ값을 대입하면 수식이 아주 단순해지는 것을 볼 수 있다.
- Step4. 최종변수에 대입해 보기
- CUPED의 최종 변수였던 Delta 값에 동일한 수식을 대입하면, 결국 ρ값에 의해서 변동성을 최종적으로 제어할 수 있다는 것을 알 수 있다.
CUPED의 통계 로직을 요약해 보면, 실험과 완전 관련 없는 변수 X를 대입하고, 우리의 종속변수 Y와 변수 X 간의 공변량을 가장 최소화시킬 수 있는 ρ 값을 찾는 과정이라고 할 수 있다.
5. CUPED 코드로 구현하기
※ Reference 공유
코드로 구현한 부분은 mtrencseni의 github와 블로그 아티클을 참조하였음을 사전에 밝힌다. 보다 더 자세한 수식 및 코드 튜닝을 위해서는 위의 언급한 블로그 글을 정독하기를 권장한다.
✅ 샘플 데이터 생성 코드
샘플 데이터는 아주 단순하게, 실험 이전의 변수 X에 대한 평균과 표준편차를 계산한다. 그런 다음에 Treatment에 대한 효과를 가정하고 이후 N개의 데이터를 생성하는 로직이다. 꽤 단순하니 이해하기에는 편할 것이라 생각한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
def get_AB_samples(before_mean, before_sigma, eps_sigma, treatment_lift, N):
A_before = list(normal(loc=before_mean, scale=before_sigma, size=N))
B_before = list(normal(loc=before_mean, scale=before_sigma, size=N))
A_after = [x + normal(loc=0, scale=eps_sigma) for x in A_before]
B_after = [x + normal(loc=0, scale=eps_sigma) + treatment_lift for x in B_before]
return A_before, B_before, A_after, B_after
N = 1000
before_mean = 100
before_sigma = 50
eps_sigma = 20
treatment_lift = 2
A_before, B_before, A_after, B_after = get_AB_samples(before_mean, before_sigma, eps_sigma, treatment_lift, N)
|
cs |
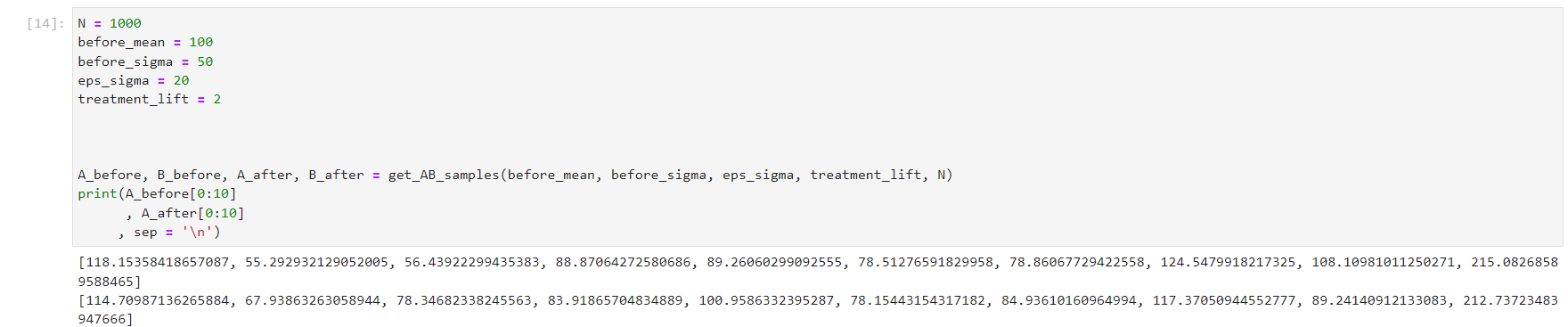
이렇게 하면 실험 이전 데이터 X를 계산하였고, 우리의 관심사인 종속변수 Y에 대한 것을 Group별로 구현하였다. 다음 단계는 이 데이터를 CUPED 모델에 학습시키고 결과를 빈도주의 결괏값과 비교해 보는 것이다.
✅ CUPED 1회 실행해 보자
1회 시행하는 것 또한 코드는 꽤 단순하다. 위의 통계수식에서 핵심은 Theta값을 이용하여 값들을 튜닝하는 것에 있었다. 그렇기 때문에 코드의 길이 또한 짧게 구현할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
def get_cuped_adjusted(A_before, B_before, A_after, B_after):
cv = cov([A_after + B_after, A_before + B_before])
theta = cv[0, 1] / cv[1, 1]
mean_before = mean(A_before + B_before)
A_after_adjusted = [after - (before - mean_before) * theta for after, before in zip(A_after, A_before)]
B_after_adjusted = [after - (before - mean_before) * theta for after, before in zip(B_after, B_before)]
return A_after_adjusted, B_after_adjusted
A_after_adjusted, B_after_adjusted = get_cuped_adjusted(A_before, B_before, A_after, B_after)
print('A mean before = %05.1f, A mean after = %05.1f, A mean after adjusted = %05.1f' % (mean(A_before), mean(A_after), mean(A_after_adjusted)))
print('B mean before = %05.1f, B mean after = %05.1f, B mean after adjusted = %05.1f' % (mean(B_before), mean(B_after), mean(B_after_adjusted)))
print('Traditional A/B test evaluation, lift = %.3f, p-value = %.3f' % (lift(A_after, B_after), p_value(A_after, B_after)))
print('CUPED adjusted A/B test evaluation, lift = %.3f, p-value = %.3f' % (lift(A_after_adjusted, B_after_adjusted), p_value(A_after_adjusted, B_after_adjusted)))
|
cs |
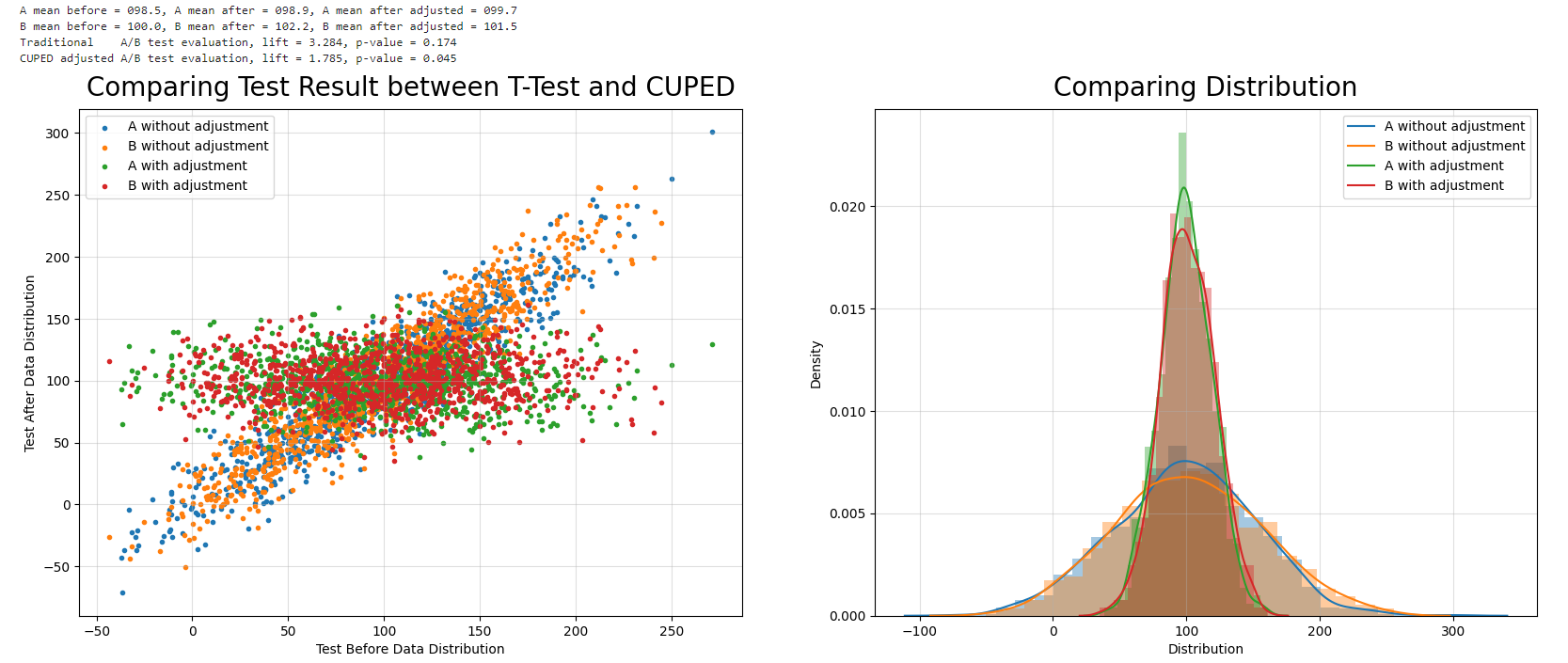
CUPED를 적용했을 때는 그 효과가 굉장히 개선되는 것을 볼 수 있다. 우선 T-Test의 P-value 값이 이전에는 0.17 수준으로 유의하지 않음을 알 수 있다. 그러나 CUPED를 적용했을 때는 P-value가 0으로 수렴하면서 두 집단 간의 평균 차이를 확실하게 발라볼 수 있었다.
이 결과가 왜 가능했는지 그래프를 살펴보면 확실하게 알 수 있다. Before Test의 값들을 보면 A와 B 모두 우상향으로 편향되어 있는 것을 볼 수 있다. 그러나 CUPED를 적용해서 Tuning 한 값을은 Before Test 값들과는 독립적이게 일정 수준에서 수평선을 이루는 것을 볼 수 있다. 이와 동시에 빨간색과 초록색 점들의 분포가 훨씬 개선되어서 평균차이를 더 확실하게 발라서 볼 수 있던 것이다.
이 결과를 CUPED 학습 이전과 이후 결과를 비교해 보면 굉장히 직관적으로 이해할 수 있다. 학습 이전에는 Group A와 Group B의 데이터 분포가 굉장히 넓은 것을 볼 수 있다. 이는 이전에 계속 다루어왔던 것처럼 모델 결과 값이 안 좋은 영향을 줄 수밖에 없는 구조이다. 반대로 CUPED로 개선한 이후에는 평균은 동일하지만, 변동성을 아주 성공적으로 개선한 것을 볼 수 있다. 두 개 Group의 분산 값이 낮아지고 개선되면서 두 집단 간 평균 차이를 아주 성공적으로 감지해 낼 수 있던 것이다.
✅ CUPED를 앞으로 어떻게 더 잘 활용할 수 있나요?
이것은 실험이 다 끝나고 난 뒤에 1회 결과를 해석한 것이다. 만약에 실험 중간에 계속 P-value를 확인할 수 있다면 더욱 활용도가 높을 것이다. 왜냐하면 더 빠르고 확실하게 P-value를 확인할 수 있기 때문에 적은 Sample Size만 수집해도 A/B Test의 Winner Call을 볼 수 있기 때문이다. 이것은 논문의 실험 결과를 발췌하여 소개하고자 한다.
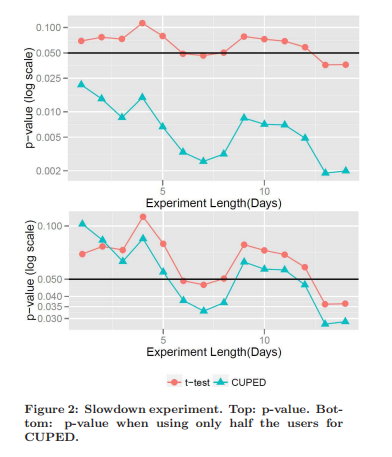
논문에서는 Bing 웹사이트에서 실제 실험을 진행했었는데, 일반 빈도주의와 CUPED의 P-value 값은 확연하게 다른 것을 볼 수가 있었다. 이렇게 실험결과를 빠르게 확인할 수 있다면, Sample Size를 절약할 수 있고 이는 자연스럽게 실험 비용을 Save 할 수 있는 사항도 될 것이다.

