E-commerce에서 가장 많이 하는 데이터 분석 업무 중 하나가 바로 A/B Test이다. 빈도주의 관점에서 실행할 수 있는 모델링 중 가장 기초적이면서도 바로 실무에 활용할 수 있는 모델이 독립표본 T-test이다. 이번 포스팅에서는 모델에 대한 기본 소개, 가설부터 시작하여 예제 코드까지 다루어볼 예정이다.
목차
1. E-commerce 환경에서 A/B Test의 기본적인 소개
2. 독립표본 T-Test의 소개 및 기본 가설
3. A/B Test 환경에서 실행하는 독립표본 T-Test
1. E-commerce 환경에서 A/B Test의 기본적인 소개
🔎 A/B Test라는 것은 무엇이며, 왜 필요하나요?

쉬운 버전으로 말하면, A/B Test은 기본적으로 두 가지 대안이 있을 때, 어떤 옵션이 더 나은 성과를 보여주는지 진행하는 실험이다. 예를 들어서, 위의 나무 이모티콘 중 앱에서 어떤 이모티콘이 더 나을지 판단해야 하는 상황이라고 해보자. 누구는 야자수 나무가 더 매력적이라고 할 수 있고, 일반적인 나무가 더 매력적이라고 하는 사람들이 있을 수 있다. 하지만 다들 자신들의 주장일 뿐 객관적인 근거가 없다. 이런 상황에서 갈등이 지속되면 발전적인 논의가 불가능하고, 결국 목소리 큰 사람의 의견대로 될 것이 자명하다.
A/B Testing의 필요성은 회사나 조직에서 의사결정을 할 때, 객관적인 데이터에 근거해서 소비자들이 실제로 어떤 대안을 좋아하는지, 비즈니스에 어떤 것이 더 더움이 되는지 판단할 수 있는 근거를 제공하는 역할을 해주기에 많은 회사들에서 채택하고 있다.
🔎 빈도주의 모델로 바라본 A/B Test 모델링
이번에는 조금 더 통계적인 관점에서 A/B Testing 모델링을 생각해보려 한다. 우선 상황을 바라보면, 독립변수는 Group에 해당하며 척도로 따지면 명목 척도(Nominal Scale)에 해당하고, 종속변수는 각 실험의 성공 지표로 보통은 CTR(클릭률) 또는 전환율(CVR)을 활용하게 되어 비율 척도(Ratio Scale)를 활용하게 된다.
E-commerece 환경에서 설정하는 가설 또한 굉장히 단순하다. 아래의 경우를 한 번 살펴보자.
- E-commerce의 A/B Testing에서 설정하는 가설
- 귀무가설(H0): Control Group's Metric(CVR, CTR) <= Treatment Group's Metric(CVR, CTR)
- 대립가설(H1): Control Group's Metric(CVR, CTR) > Treatment Group's Metric(CVR, CTR)
이렇게 가설을 설정하는 이유는 굉장히 단순하다. 왜냐하면 새로 출시하는 Feature나 디자인이 기존 것보다 효과성이 떨어진다면 굳이 출시할 이유가 없기 때문이다. 또한 위의 가설로 실험했을 때 나중에는 기대수익과 기대손실까지 계산해 낼 수 있기 때문에 A/B Testing을 실행하게 된다.
독립변수는 명목척도에 종속변수는 비율척도인 상황에서 가설 검정을 위해서 채택할 수 있는 대표적인 모델은 T-Test와 Z-test가 있다. 또한 CVR과 CTR은 사실 0과 1로 이루어진 이항분포로도 볼 수 있기 때문에 카이제곱(chi-square) 모델링으로도 검증이 가능하다. 오늘은 이 모델들에 대해서 기본적인 개념과 실행하는 방법에 대해서 소개해보도록 하겠다.
※ 참고 사항 - 독립변수가 3개 이상이되면 ANOVA를 실행해야 하지만, 이번 포스팅 주제와 다소 거리가 멀어질 것 같아 다른 포스팅에서 다루어보겠다.
2. 독립표본 T-Test의 소개 및 기본 가설
🔎 T-Test는 무엇인지 간단하게 설명해줄 수 있나요?
Independent T-Test(독립표본 T-Test)는 두 집단 평균 차이가 유의한 지 밝히는 대표적인 모델이다. 다른 이름으로는 Student T-Test라고 불리며, 많은 사회과학 논문에서 채택되고 있는 방법이다. 기본적으로 두 개의 표본으로부터 추정된 분산을 기반으로 두 집단 간 평균에 차이가 있는지 없는지를 밝혀내는 모델링이라고 이해하면 된다.
- T-Test의 귀무가설과 대립가설
- 귀무가설: Control's CVR = Treament's CVR
- 대립가설: Control's CVR ≠ Treatment's CVR
- T-Test에서 지켜야 하는 기본적인 과정
- 변수들의 분포는 양측대칭이어야 하는 특징이 있다.
- 변수들의 분포는 등분산성을 가져야 한다.
가설에서 볼 수 있듯이, T-Test는 두 집단 간 차이가 있는지를 알려주는 모델이지, 어떤 그룹이 더 높거나 얼마나 높은지 보여주는 모델이 아니다. 따라서 T-Test 결과가 나왔다고 해서 무조건적으로 Treatment Group이 평균적으로 더 높다고 해석하면 안 된다. Test 이후에 Effect Size에 대한 탐구는 더 심도 있는 분석을 통해서 밝혀내야 한다. 보통은 두 그룹의 분포를 그려보고, 이에 대한 기술 통계값을 내본다음에 최종적으로 Control을 선택할지 Treatment를 선택할지 밝히는 것이 일반적이다.
참고로 T-Test에도 여러가지 종류가 있는데, 이번 포스팅 주제와는 다소 결이 다르니 다른 포스팅에서 조금 더 자세히 다루어볼 예정이다.
3. A/B Test 환경에서 실행하는 독립표본 T-Test
🔎 A/B Testing에 상황을 통한 T-Test 활용의 이해
- T-Test(Independent T-Test)로 A/B Test를 검증하는 과정
- Step1. 실험을 통해 대응되는 표본 2개에서 데이터를 수집
- Step2. 각 표본의 데이터가 정규 분포를 이루고 있는지 검증
- Step3. 두 개의 표본 데이터가 등분산성을 이루고 있는지 검증
- Step4. Independent T-test를 통해서 두 개의 집단 간 평균차이가 있는지 검증
- Step5. 기술통계 및 분포를 확인하여 평균 차이를 계산
위에서 말한 5가지 과정을 거치면 독립표본 T-Test를 활용한 A/B Test를 검증할 수 있다. 각각의 과정을 Code로 설명해보고자 한다. 사실 Step1은 데이터를 수집하는 과정이라 임의의 데이터를 생성하여 대체하는 것으로 하겠다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
## Step1. 실험 데이터 생성
#control
mu_0 = 0.54
std_0 = 0.031
#treatment
mu_1 = 0.62
std_1 = 0.032
## 표본 사이즈 결정
sample_size = 1000
##
control = stats.norm(mu_0, std_0).rvs(sample_size)
treatment = stats.norm(mu_1, std_1).rvs(sample_size)
|
cs |
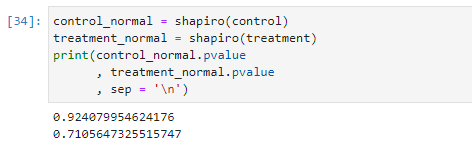
두 번째 과정은 각 표본이 정규 분포를 형성하고 있는지 검증하는 과정이다. 이번 포스팅에서는 Shapiro 테스트를 통해서 정규성을 검증할 것이다. 주의할 점은 Shaprio 테스트는 P-value가 0.05 초과여야지 정규성이 확보가 되는 것이기 때문에 수치해석에 주의가 필요하다.
|
1
2
3
4
5
6
|
## 각 표본의 정규성
control_normal = shapiro(control)
treatment_normal = shapiro(treatment)
print(control_normal.pvalue
, treatment_normal.pvalue
, sep = '\n')
|
cs |
세 번째 과정은 두 표본이 등분산성을 이루고 있는지 확인하는 것이다. 이번에는 Levene 모델을 활용하여 검증할 예정이다. 여기에서도 주의할 점은 Levene 테스트의 p-value가 0.05 초과여야 등분산성이 확보가 된 것이다. 결과 해석 시 주의가 필요한 부분이다.
|
1
2
3
4
|
# 등분산성 고려
from scipy.stats import levene
print(levene(control, treatment))
|
cs |

네 번째 과정은 대응 표본 T-Test 결과를 해석하는 것이다. 모델은 scipy.stats에 등록되어 있는 모델을 활용하였다. 아래의 사진을 보면 P-value가 0.05보다 훨씬 작은 숫자를 기록하였다. 따라서 두 모델 간 평균에는 차이가 확실하게 있는 것으로 볼 수 있다. 하지만 여기서도 아직 누구의 평균이 더 큰지는 모르는 것이기 때문에 주의해야 한다.

마지막 과정은 실제 기술통계값을 확인하고 분포를 그려봐서, 누가 얼마나 더 높은지 확인을 해야 하는 과정을 거쳐야 한다. 아래의 사진을 보면 약 0.08 즉 8%의 전화율 차이를 보여주는 실험 결과를 확인할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
plt.rcParams['figure.figsize'] = (8, 6)
sns.distplot(control)
sns.distplot(treatment)
plt.title('CVR Distribution of the Experiment', fontsize = 15, pad = 10)
plt.legend(['control', 'treatment'])
plt.axvline(control.mean(), linestyle = '--')
plt.axvline(treatment.mean(), linestyle = '--', color = 'r', alpha = 0.5)
plt.grid(alpha = 0.4);
|
cs |
 |
 |
여기까지 독립표본 T-Test를 활용해서 어떻게 A/B Test를 실행할 수 있는지에 대해서 알아보았다. 사실 다른 많은 방법들이 존재하고, 이는 그중 한 가지일 뿐이니 참고하기를 바란다.
'통계학 기초' 카테고리의 다른 글
| 회귀모델 평가를 위한 통계 오차 지표 모음(MSE, MAE, RMSE 등 5개 지표) (1) | 2024.02.06 |
|---|---|
| [Python]이원분산분석(Two-way ANOVA) 코드부터 결과 해석 가이드 (1) | 2022.09.15 |
| [Python] 카이제곱 독립성 검정을 활용한 데이터 분석(feat. A/B Test까지) (0) | 2022.08.30 |
| [Python] COHORT 분석 개념부터 실전 코드까지 (feat. 분석 예제 포함) (0) | 2022.08.18 |
| [Python]베이지안 A/B Test로 기대수익과 기대손실 계산하는 방법 (0) | 2022.08.11 |



