1. DFS의 기본 개념
2. 스택/큐를 활용한 DFS 구현하기
3. 재귀함수를 이용한 DFS 구현하기
1. DFS의 기본 개념
(1) 기본개념
DFS란 Depth first search의 약자로서 그래프 자료에서 데이터를 탐색하는 알고리즘입니다.
한 번 예시를 들어 보겠습니다.
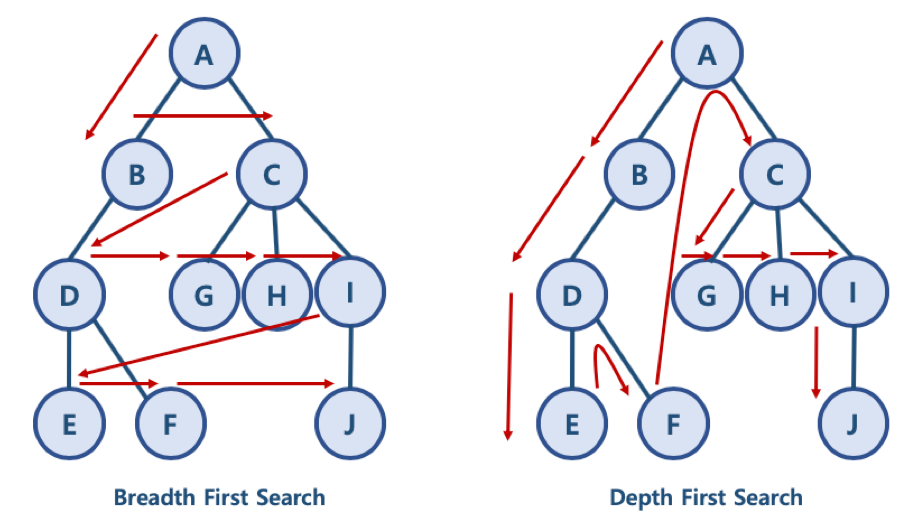
오른쪽에 보이다 싶이 A부터 J까지 노드가 연결되어 있는 그래프 자료를 볼 수 있습니다. 그래프에서 특정 노드를 찾으려고 할 때, 위에서 부터 찾느냐 혹은 옆에서부터 찾느냐 그 차이가 있겠죠.
위에서 아래로 찾는 방식을 바로 DFS(Depth First Search)라고 부르는 것입니다.
BFS(Breadth First Search)는 차후 포스팅에서 다루도록 하겠습니다.
참고로 위에서 아래로 탐색할 때 왼쪽으로 가냐 오른쪽으로 가냐는 전혀 상관 없습니다~
데이터 입력하기 귀찮으신 분들은 아래의 코드 복붙해주세요.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
|
cs |
(2) DFS의 기본 원칙
DFS에서 데이터를 찾을 때는 항상 "앞으로 찾아야 가야할 노드"와 "이미 방문한 노드"를 기준으로 데이터를 탐색을 합니다.
이 원칙을 반드시 기억해주셔야 해요.
그래서 특정 노드가 "앞으로 찾아야 가야할 노드"라면 계속 검색을 하는 것이고, "이미 방문한 노드"면 무시하거나 따로 저장하면 됩니다.
(3) DFS의 구현 방식
DFS를 구현할 때는 기본적으로 "스택/큐"를 활용할 수도 있고, "재귀함수를 통해 구현할 수도 있습니다. 두 가지 방법 모두 아래의 부분에서 소개해드리도록 하겠습니다.
2. 스택/큐를 활용한 DFS 구현
(1) 리스트를 활용한 DFS 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
def dfs(graph, start_node):
## 기본은 항상 두개의 리스트를 별도로 관리해주는 것
need_visited, visited = list(), list()
## 시작 노드를 시정하기
need_visited.append(start_node)
## 만약 아직도 방문이 필요한 노드가 있다면,
while need_visited:
## 그 중에서 가장 마지막 데이터를 추출 (스택 구조의 활용)
node = need_visited.pop()
## 만약 그 노드가 방문한 목록에 없다면
if node not in visited:
## 방문한 목록에 추가하기
visited.append(node)
## 그 노드에 연결된 노드를
need_visited.extend(graph[node])
return visited
|
cs |
여기서는 need_visited에서 추가된 Node들 중에서 가장 끝에 있는 것을 뽑아서 검색하는 방식입니다. 바로 이것이 "스택"을 활요한 방식이죠.
파이썬은 굉장히 편한 언어라서 리스트로도 쉽게 구현할 수 있습니다. 다만 list에서 pop을 활용하면 성능면에서 떨어지는 단점이 있어요.

(2) deque를 활용한 DFS 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
def dfs2(graph, start_node):
## deque 패키지 불러오기
from collections import deque
visited = []
need_visited = deque()
##시작 노드 설정해주기
need_visited.append(start_node)
## 방문이 필요한 리스트가 아직 존재한다면
while need_visited:
## 시작 노드를 지정하고
node = need_visited.pop()
##만약 방문한 리스트에 없다면
if node not in visited:
## 방문 리스트에 노드를 추가
visited.append(node)
## 인접 노드들을 방문 예정 리스트에 추가
need_visited.extend(graph[node])
return visited
|
cs |
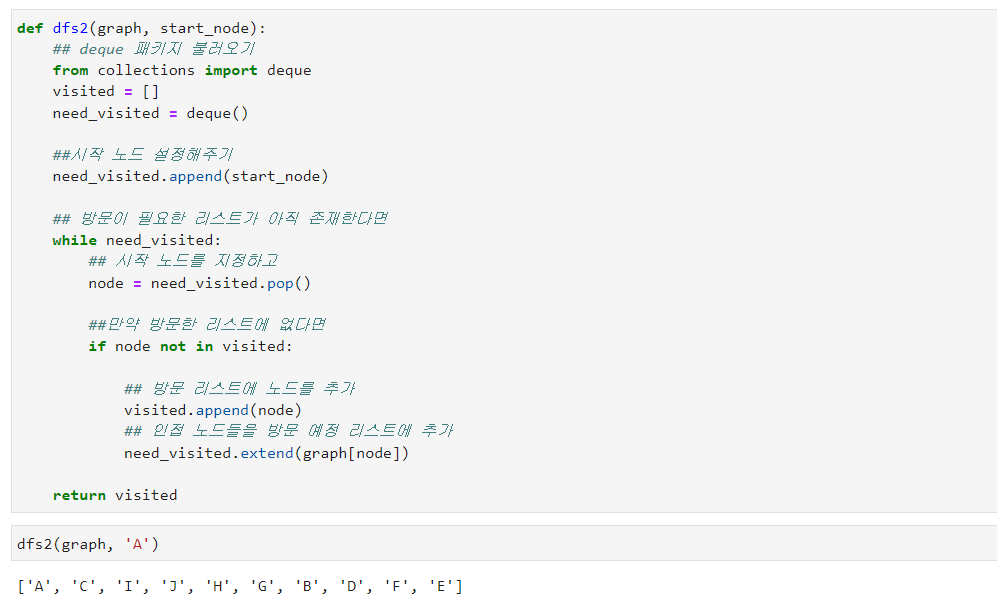
스택/큐를 구현할 때는 collections라는 패키지에서 deque를 활용하시는 것을 추천드립니다.
논리는 거의 동일합니다만, 성능면에서 list() 형태보다 deque형태가 훨씬 좋아요!!
3. 재귀함수를 통한 DFS 구현
|
1
2
3
4
5
6
7
|
def dfs_recursive(graph, start, visited = []):
## 데이터를 추가하는 명령어 / 재귀가 이루어짐
visited.append(start) for node in graph[start]:
if node not in visited:
dfs_recursive(graph, node, visited)
return visited
|
cs |
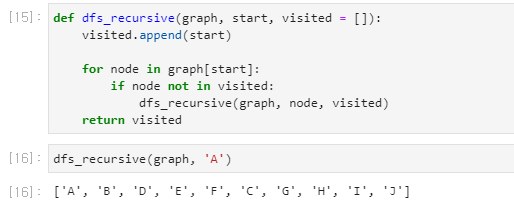
재귀함수를 통해서 DFS를 구현해봤습니다.
특징 정인 것은 visited 자료형을 기본 함수 인자로 포함시키고, 방문한 리스트들을 재귀함수를 통해서 계속 visited에 담는 방식입니다.
훨씬 단순한 구조이지만, 재귀함수를 이해하지 못 하면 어려워 보일 수도 있죠. 저는 개인적으로 재귀함수를 DFS 구현할 때 많이 활용합니다.
'Python > 알고리즘' 카테고리의 다른 글
| [Python]버블정렬 알고리즘 코드 및 예시로 마스터 하기 (0) | 2022.08.23 |
|---|---|
| BFS 완벽 구현하기 - 파이썬 (0) | 2021.02.01 |
| 그래프의 이해 - 고도 알고리즘을 위한 기초 개념 (0) | 2021.01.17 |
| 탐색 알고리즘 - 이진 탐색 (0) | 2021.01.11 |
| 탐색 알고리즘 - 순차 탐색(Sequential Search) (0) | 2021.01.09 |


